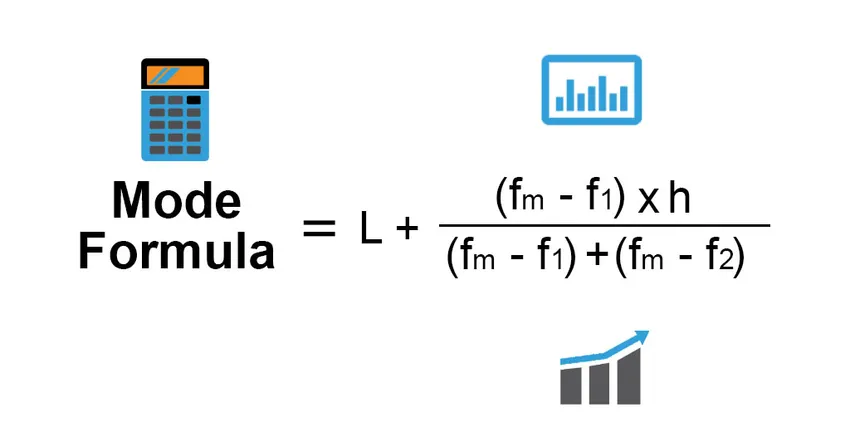
Formule de mode (table des matières)
- Formule
- Exemples
- Calculatrice
Qu'est-ce que la formule mode?
Les trois mesures centrales de tendance sont la médiane moyenne et le mode. Lorsque les trois sont utilisés ensemble pour extraire une analyse significative dans l'ensemble de données. Aujourd'hui, dans cet article, nous allons discuter du mode qui est également l'une des clés et de la tendance centrale de la méthode importante utilisée. Le mode fait référence à la valeur la plus fréquemment rencontrée dans l'ensemble de données. Le mode d'une donnée peut être trouvé avec un ensemble de données normal, un ensemble de données de groupe ainsi qu'un ensemble de données non groupé ou non groupé. Cependant, la moyenne la plus couramment utilisée reste la meilleure mesure de la tendance centrale malgré l'existence de la moyenne, de la médiane et du mode. Dans cet article, nous allons essayer de comprendre la fonction mode, des exemples et des explications de chaque exemple ainsi que la formule et les calculs.
La formule pour le mode est: -
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Formule de mode pour les données groupées:
Mode = L + (fm − f1) h / 2fm − f1 − f2
Où,
- L = Mode limite inférieure de la classe modale
- fm = Fréquence de la classe modale
- f1 = Fréquence de la classe précédant la classe modale
- f2 = Fréquence de classe succédant à la classe modale
- h = taille de l'intervalle de classe
Exemples de formule de mode (avec modèle Excel)
Prenons un exemple pour mieux comprendre le calcul du mode.
Vous pouvez télécharger ce modèle Excel de formule de mode ici - Modèle Excel de formule de modeFormule de mode - Exemple # 1
Où le mode est calculé simplement le nombre d'observations dans un ensemble de données qui se produit la plupart du temps.
Calculez le mode de l'ensemble de données suivant.
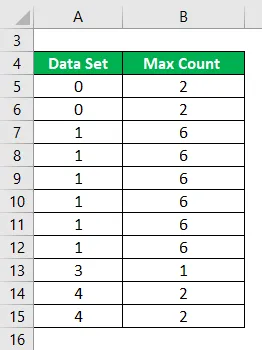
Solution:
Un mode est calculé comme suit:
Nombre d'observations dans un ensemble de données qui se produisent la plupart du temps
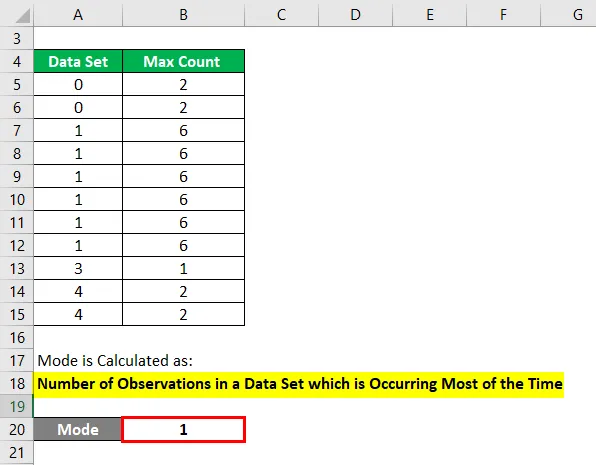
- Mode = 1
Formule de mode - Exemple # 2
Calculez le mode en utilisant les informations fournies.
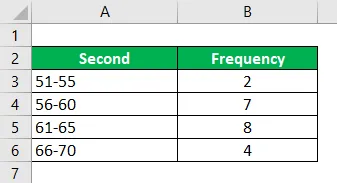
Solution:
Remarque: - Tout d'abord, le groupe modal avec la fréquence la plus élevée doit identifier Si l'intervalle n'est pas continu, 0, 5 doit être soustrait du mode de limite inférieure et 0, 5 doit être ajouté du mode de limite supérieure. Ensuite, l'intervalle sera
Le groupe modal est calculé comme suit:
Groupe modal le plus fréquent, c.-à-d. 60, 5-65, 5
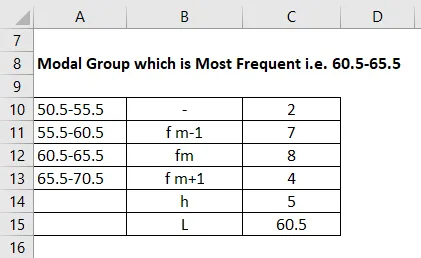
Ensuite, la fréquence la plus basse est du groupe modal qui est 4, dans ce cas, est pris comme fm + 1 et fm-1 deviendra 7 dans cet exemple. Et nous avons fm qui est la fréquence de 8. Le (h) est appelé la taille de l'intervalle de classe est 5 que nous avons également en considérant l'intervalle de départ. L est 60, 5.
Le mode est calculé en utilisant la formule donnée ci-dessous
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
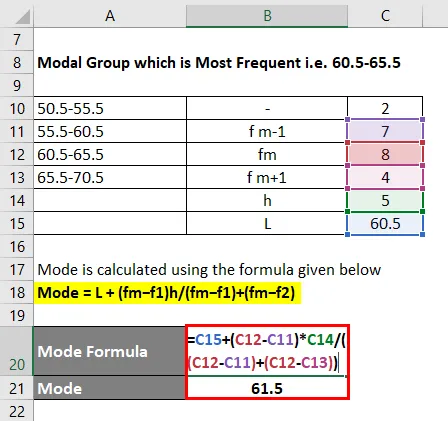
- Mode = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Mode = 61, 5
Formule de mode - Exemple # 3
Voici les répartitions des hauteurs dans une certaine classe d'élèves dans un certain mode
Calculez le mode en utilisant les informations fournies.
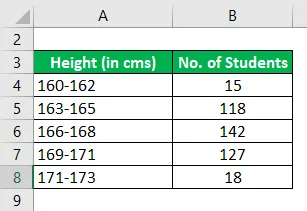
Solution:
Si l'intervalle n'est pas continu, 0, 5 doit être soustrait du mode de limite inférieure et 0, 5 doit être ajouté du mode de limite supérieure. Ensuite, l'intervalle sera
Le groupe modal est calculé comme suit:
Groupe modal le plus fréquent (165, 5-168, 5)
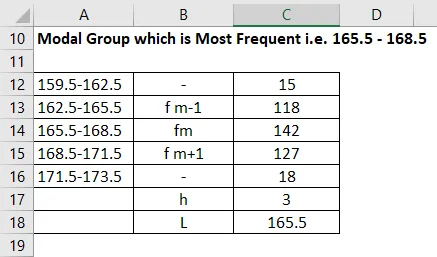
Le mode est calculé en utilisant la formule donnée ci-dessous
Mode = L + (fm − f1) h / (fm − f1) + (fm − f2)
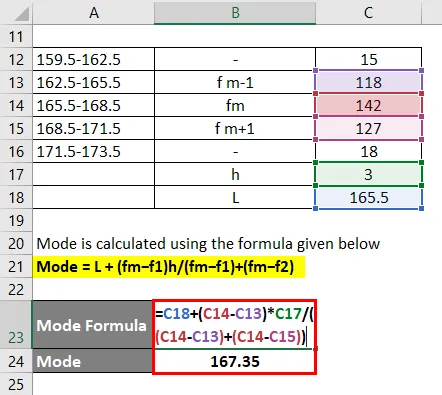
- Mode = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Mode = 167, 35
Explication
Le mode peut être simplement expliqué comme la valeur la plus fréquente dans l'ensemble de données. Et le mode ci-dessus peut être expliqué comme lorsque les données sont un groupe, nous devons d'abord calculer la fonction modale et également rendre les données continues afin de calculer le mode des données. La classe modale est décidée avec la classe qui a la fréquence la plus élevée dans l'ensemble de données.
Pertinence et utilisations de la formule Mode
- La moyenne, la médiane et le mode révèlent différents aspects de vos données. N'importe qui vous donnera une idée générale, mais peut vous induire en erreur; avoir les trois vous donnera une image plus complète
- Pour une distribution normale, le mode, la moyenne et la médiane ont la même valeur car le mode est une distribution normale. Le mode d'analyse isolé ne reflète pas la vraie image, si vous souhaitez analyser l'ensemble de données complet, les trois mesures statistiques doivent être analysées en détail et interprétées
- Le mode est facile à comprendre et simple à calculer.
- Le mode n'est pas affecté par des valeurs extrêmement grandes ou petites.
- Le mode peut être localisé simplement par inspection dans des données non groupées et une distribution de fréquence discrète.
- Le mode peut être utile pour les données qualitatives.
- Le mode peut être calculé dans une table de fréquences ouverte.
- Le mode peut être localisé graphiquement
- Le mode est utilisé par les scientifiques des données le plus souvent
- Le mode est qu'il ne nous fournira pas une très bonne mesure de la tendance centrale lorsque la marque la plus courante est loin du reste des données dans l'ensemble de données
Calculateur de formule de mode
Vous pouvez utiliser le calculateur de formule de mode suivant
| L | |
| fm | |
| f1 | |
| f2 | |
| h | |
| Formule de mode | |
| Formule de mode = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Articles recommandés
Ceci est un guide de la formule de mode. Ici, nous discutons de la façon de calculer la formule de mode avec des exemples pratiques. Nous fournissons également une calculatrice de mode avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Exemples de la formule du modèle de croissance Gordon
- Formule pour calculer le modèle de tarification des immobilisations
- Calculatrice pour la formule du ratio des dépenses totales
- Formule de distribution de Poisson (exemples avec modèle Excel)