
Différence entre le score Z et le score T
Le score Z est une conversion des données brutes en un score standard, lorsque la conversion est basée sur la moyenne de la population et l'écart-type de la population. Lorsqu'un ensemble de données complet est disponible avec nous, nous pouvons calculer le score Z. Le score Z est la soustraction de la moyenne de la population du score brut, puis divise le résultat par l'écart-type de la population. Le score T est une conversion des données brutes en score standard lorsque la conversion est basée sur la moyenne de l'échantillon et l'écart-type de l'échantillon. Lorsque l'ensemble de données sur la population n'est pas disponible, nous devons collecter des données d'échantillonnage pour calculer la moyenne de l'échantillon et l'écart type de la population.
Score Z
Dans une distribution normale, où des données complètes sont disponibles, c'est une distance de la moyenne. Sa formule est la suivante,
Z= (x-μ)/σ
Où,
X = données brutes individuelles
μ = moyenne de la population
σ = écart type de la population
Score T
Le score T est la soustraction de l'écart-type individuel de la moyenne individuelle, puis divise le résultat par le résultat entier de l'écart-type de l'échantillon multiplié par la taille de l'échantillon. Sa formule est la suivante,
t = ((- μ)/s)*
= Échantillon moyen
μ = Moyenne de la population
s = Écart type d'échantillon
n = taille de l'échantillon
Prenons un exemple pour mieux comprendre la même chose:
Dans un document, 3 subdivisions sont là-I, II et III. Supposons que le nombre d'élèves qui ont répondu I soit correctement de 25%, c'est-à-dire que 75% ne sont pas en mesure de répondre correctement. De même, laissez 10% et 20% par le nombre de personnes ayant répondu correctement aux sections II et III, donc 90% et 80% ont trouvé les sections II et III cependant. Nous supposons que la capacité mesurée par ces trois éléments est la même et qu'elle est normalement distribuée,
Le score de chaque élève d'une classe est utilisé pour calculer la moyenne des notes qui est égale à 50 et un écart-type de 10. Nous pouvons calculer le score Z avec le score de 50 comme (50-50) / 10 = 0
Nous pouvons interpréter que le score de l'élève est à 0 distance (en unités d'écarts-types) de la moyenne, de sorte que l'élève a obtenu une moyenne.
Si le score est 60, le score Z est (60-50) / 10 = 1
Nous pouvons interpréter que l'élève a obtenu un score supérieur à la moyenne - une distance de 1 écart-type au-dessus de la moyenne.
Comparaison directe entre le score Z et le score T (infographie)
Ci-dessous, la différence entre le score Z et le score T 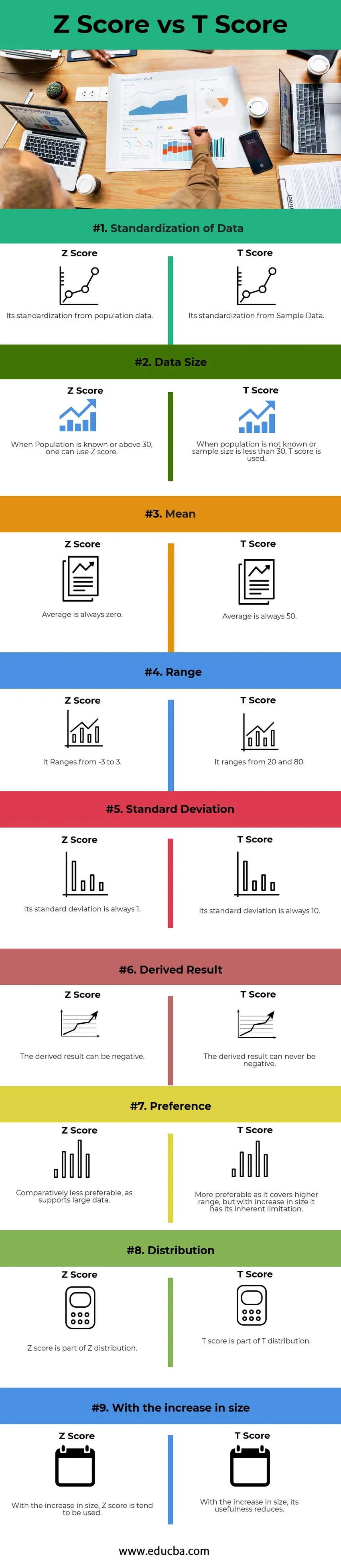
Différences clés entre le score Z et le score T
Voyons quelques-unes des principales différences entre le score Z et le score T
- Le score Z est la standardisation des données brutes de la population ou plus de 30 échantillons de données au score standard tandis que le score T est la standardisation des données de l'échantillon de moins de 30 données au score standard
- Le score Z varie de -3 à 3, tandis que le score T varie de 20 à 80.
- À mesure que la taille des données augmente, la distribution tend à être une distribution Z. La distribution du score Z par rapport au score T fait partie d'une distribution normale, mais en fonction de la taille, ils diffèrent l'un de l'autre
- En pratique, le score Z est largement utilisé dans les données boursières et pour vérifier les chances d'une entreprise de faire faillite, tandis que le score t est largement utilisé pour vérifier la densité minérale osseuse et les évaluations des risques de fracture
Tableau de comparaison du score Z par rapport au score T
Regardons le top 9 Comparaison entre le score Z et le score T
| Sr. No. | Points de comparaison | Score Z | Score T |
| 1 | Standardisation des données | Sa standardisation à partir des données démographiques | Sa standardisation à partir d'échantillons de données |
| 2 | Taille des données | Lorsque la population est connue ou supérieure à 30, on peut utiliser le score Z | Lorsque la population n'est pas connue ou que la taille de l'échantillon est inférieure à 30, le score T est utilisé. |
| 3 | Signifier | Une moyenne est toujours nulle. | Une moyenne est toujours de 50. |
| 4 | Gamme | Il varie de -3 à 3. | Il varie de 20 à 80. |
| 5 | Écart-type | Son écart type est toujours de 1 | Son écart type est toujours de 10 |
| 6 | Résultat dérivé | Le résultat dérivé peut être négatif | Le résultat dérivé ne peut jamais être négatif |
| sept | Préférence | Comparativement moins préférable, car prend en charge les données volumineuses | Plus préférable car il couvre une gamme plus élevée, mais avec une augmentation de taille, il a sa limitation inhérente |
| 8 | Distribution | Le score Z fait partie de la distribution Z | Le score T fait partie de la distribution T |
| 9 | Avec l'augmentation de taille | Avec l'augmentation de la taille, le score Z a tendance à être utilisé | Avec l'augmentation de taille, son utilité diminue. |
Conclusion
Le score Z par rapport au score T fait partie des tests d'hypothèse dans la distribution normale. Si vous disposez d'un ensemble de scores de mesure pour différentes mesures utilisant des scores Z, vous pouvez dire comment les scores sont placés dans leurs distributions. Ensuite, vous pouvez les comparer. La normalisation des scores est une procédure largement utilisée dans le domaine de la recherche et de la planification car elle aide à comparer les différents scores aux tests. La standardisation des scores avant de les combiner aide un chercheur à obtenir des résultats meilleurs et comparables.
Articles recommandés
Cela a été un guide pour la différence entre le score Z et le score T. Ici, nous discutons également des différences clés entre le score Z et le score T avec des infographies et un tableau de comparaison. Vous pouvez également consulter les articles suivants pour en savoir plus-
- Finance vs Economie - Top Différence
- Déficit vs dette - lequel est le meilleur
- Achat d'actifs vs achat d'actions
- Marché monétaire vs marché des capitaux
- Aperçu de Altman Z Score