Diagramme de dispersion dans Matlab
MATLAB est un langage utilisé pour l'informatique technique. Comme la plupart d'entre nous en conviendront, un environnement facile à utiliser est indispensable pour intégrer les tâches de calcul, de visualisation et enfin de programmation. MATLAB fait de même en fournissant un environnement qui est non seulement facile à utiliser mais aussi, les solutions que nous obtenons sont affichées en termes de notations mathématiques que la plupart d'entre nous connaissent. Dans cette rubrique, nous allons en savoir plus sur les diagrammes de dispersion dans Matlab.
Les utilisations de MATLAB comprennent (mais sans s'y limiter):
- Calcul
- Développement d'algorithmes
- La modélisation
- Simulation
- Prototypage
- Analyse des données (analyse et visualisation des données)
- Graphiques techniques et scientifiques
- Développement d'applications
MATLAB fournit à son utilisateur un panier de fonctions, dans cet article, nous comprendrons une fonction puissante appelée «fonction Scatter Plot»
SYNTAXE de la fonction de diagramme de dispersion:
scatter(a, b)
scatter(a, b, z)
scatter(a, b, z, c)
scatter(___, 'filled')
scatter(___, mkr)
scatter(___, Name, Value)
Maintenant, comprenons tout cela un par un:
Description des diagrammes de dispersion dans MATLAB
Voici la description des nuages de points dans la mention MATLAB ci-dessous
1. dispersion (a, b)
- Cette fonction nous aidera à faire un diagramme de dispersion avec des cercles aux emplacements spécifiés des vecteurs 'a' et 'b' mentionnés dans la fonction
- Ces types de graphiques sont également appelés «graphiques à bulles»
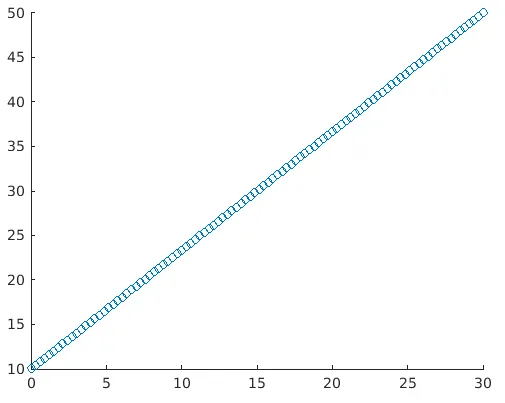
Exemple: définissons deux variables a et b
a = linspace(0, 30, 100); (This will create 100 values between 0 and 30, all equally spaced) b = linspace(10, 50, 100); (This will create 100 values between 10 and 50, all equally spaced) scatter(a, b)
Solution: nous obtiendrons le graphique suivant dans MATLAB
2. dispersion (a, b, z)
Cette fonction définira les tailles de cercle.
Les tailles de cercle suivantes peuvent être créées à l'aide de cette fonction dans les graphiques:
- Cercles de taille égale: pour créer un tracé avec un cercle de taille égale, définissez le paramètre «z» dans la fonction pour être scalaire
- Cercles de tailles différentes: pour créer un tracé avec des cercles de tailles inégales, définissez le paramètre «z» en fonction de vecteur et la longueur du vecteur étant égale à la longueur de «a» et «b»
Exemple
Prenons le même exemple que dans l'explication précédente, pour garder les choses simples pour une meilleure compréhension
a = linspace(0, 30, 100);
b = linspace(10, 50, 100);
z = linspace(1, 100, 100); (Here we are passing the z parameter as a vector, so our graph will have circles of different sizes) scatter(a, b, z)
Solution : nous obtiendrons le graphique suivant dans MATLAB
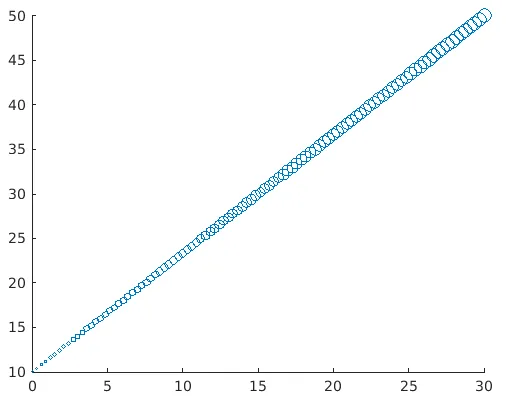
Nous pouvons clairement visualiser que les cercles du graphique sont de tailles différentes. L'importance de faire cela est que nous attirerons immédiatement notre attention vers des valeurs plus élevées.
3. dispersion (a, b, z, c)
Cette fonction définira la couleur des cercles à tracer dans le graphique.
Cela aidera à spécifier la couleur comme suit:
- Pour les cercles de même couleur, définissez «c» comme le nom de la couleur d'un triplet RVB
- Pour les cercles de couleurs différentes, définissez «c» comme une matrice tricolore sur un triplet RVB ou un vecteur
Exemple:
a = linspace(0, 30, 100);
b = linspace(10, 50, 100);
c = linspace(1, 10, length(x));
scatter(a, b, ( ), c)
Solution : nous obtiendrons le graphique suivant dans MATLAB
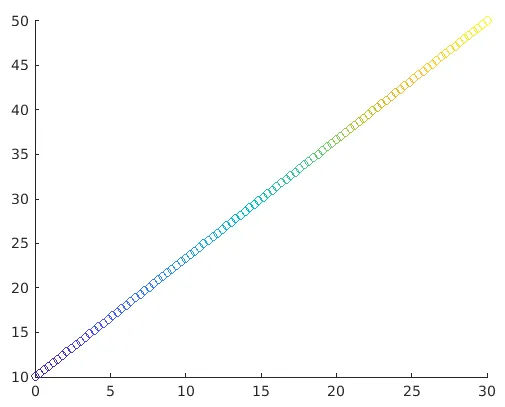
Ici, les éléments présents dans a, b et c détermineront l'emplacement et la couleur des cercles. Et puis la fonction scatter aidera à mapper les éléments présents en c aux couleurs présentes dans la palette de couleurs.
Nous pouvons visualiser clairement des cercles de couleurs changeantes. Cela nous aide à différencier les valeurs supérieures et inférieures selon nos besoins
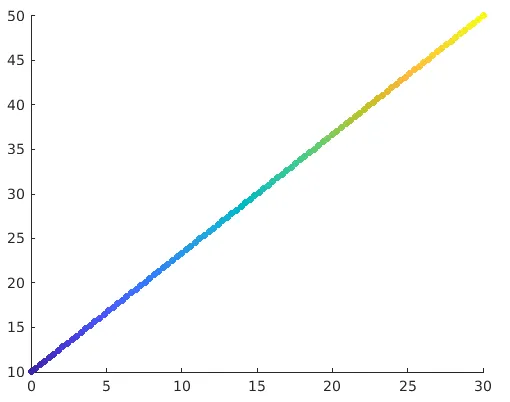
4. scatter (___, «rempli»)
Maintenant, que faire si nous avons besoin que tous ces cercles soient solides ou en d'autres termes, remplis de couleurs. Cette fonction vous aidera à remplir les cercles. Nous avons juste besoin de passer l'argument «rempli» dans la fonction pour que les cercles soient remplis dans le graphique de nuage de points.
Exemple:
a= linspace(0, 30, 100);
b = linspace(10, 50, 100);
z = 25;
c = linspace(1, 10, length(a));
scatter(a, b, z, c, 'filled')
Solution: nous obtiendrons le graphique suivant dans MATLAB
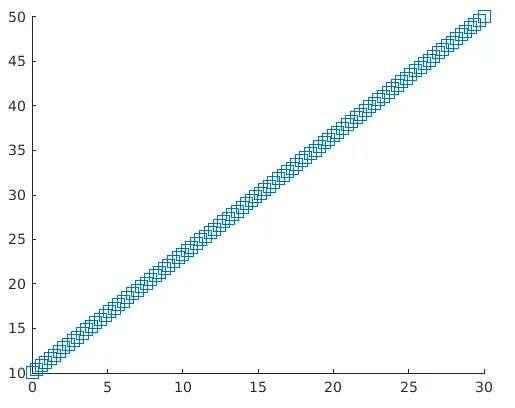
5. scatter (___, mkr)
Les formes par défaut des nuages de points sont des cercles. Si nous avons besoin d'une autre forme comme un carré, cette fonction peut être utilisée. Nous avons juste besoin de spécifier le marqueur, par exemple, nous pouvons obtenir la forme carrée avec l'argument 's' dans la fonction.
Exemple:
a = linspace(0, 30, 100);
b = linspace(10, 50, 100);
z = 140;
scatter(a, b, z, 's')
Solution: nous obtiendrons le graphique suivant dans MATLAB
6. scatter (___, nom, valeur)
Cette fonction modifiera le diagramme de dispersion pour la paire «Nom» et «Valeur» mentionnée dans l'argument. Par exemple, Linewidth, 1 définira le contour des cercles dans le tracé à 1 mm. De même, 'MarkEdgecolor' sera utilisé pour changer la couleur du contour des cercles.
Exemple:
a= linspace(0, 30, 100);
b = linspace(10, 50, 100);
sz = 40;
scatter(a, b, sz, 'MarkerEdgeColor', (0 .5 .5), …
'LineWidth', 1.5)
Solution: nous obtiendrons le graphique suivant dans MATLAB
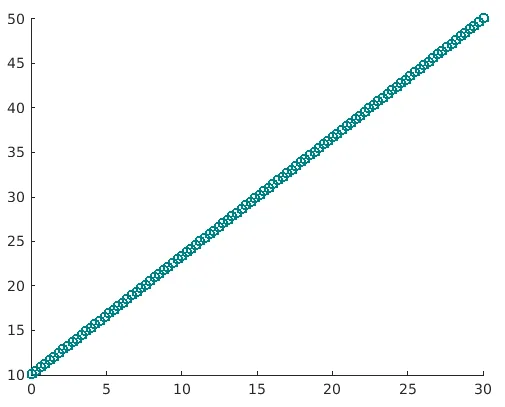
Ici, nous pouvons clairement voir que la couleur du contour a changé et que la largeur est maintenant de 1, 5
- Les diagrammes de dispersion sont des graphiques très pratiques pour obtenir l'apparence des données en les visualisant simplement
- Des diagrammes de dispersion peuvent être utilisés pour visualiser s'il existe une relation entre les valeurs des données
- Par exemple, un nuage de points avec des valeurs concentrées dans une zone particulière signifie que de nombreuses valeurs de l'ensemble de données appartiennent à cette zone
- Il permet également de visualiser les valeurs aberrantes dans les données
- De même, dans l'exemple que nous avons utilisé, nous pouvons visualiser la relation linéaire entre les variables.
- Et oui, si toutes les valeurs sont dispersées et ne suivent aucun schéma, nous pouvons être sûrs qu'il n'y a pratiquement aucune relation entre les variables que nous utilisons.
Articles recommandés
Ceci est un guide des nuages de points dans Matlab. Nous discutons ici des utilisations de MATLAB avec la description des diagrammes de dispersion. Vous pouvez également consulter l'article suivant.
- Avantages de Matlab
- Fonction moyenne dans Matlab
- Fonction de filtrage dans Matlab
- Matrix in Matlab