
Introduction à la fonction récursive en Java
Une fonction récursive est celle qui s'appelle une ou plusieurs fois. Une fonction récursive est utilisée dans les situations où le même ensemble d'opérations doit être effectué encore et encore jusqu'à ce que le résultat soit atteint. Il effectue plusieurs itérations et l'énoncé du problème devient de plus en plus simple à chaque itération.
Une limite de base doit toujours être spécifiée lors de l'écriture d'une fonction récursive, sinon elle entraîne une erreur de dépassement de pile. Une pile est une zone mémoire réservée pour maintenir les appels de méthode. L'erreur est due au fait que la fonction commence à s'exécuter en continu car elle ne pourra pas trouver la condition limite et donc épuiser finalement la mémoire allouée. Ainsi, pour éviter un débordement de pile, nous définissons certaines conditions de base à l'aide d'instructions «if… else» (ou de toute autre instruction conditionnelle), ce qui arrête la fonction de récursivité dès que le calcul requis est terminé.
Types de récursivité en Java
Il existe 2 types de récursivité en Java. Elles sont:
1. Récursivité directe
Syntaxe:
Ici, la fonction1 s'appelle continuellement, c'est donc une fonction récursive.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Exemple
La factorielle d'un nombre est un exemple de récursivité directe. Le principe de base de la récursivité est de résoudre un problème complexe en le divisant en plus petits. Par exemple, dans le cas de la factorielle d'un nombre, nous calculons la factorielle de «i» si nous connaissons sa factorielle de «i-1».
Code:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Production:

2. Récursivité indirecte / mutuelle
Une fonction1 qui appelle une autre fonction2, qui à son tour appelle la fonction1 directement ou indirectement est appelée fonction récursive indirecte.
Syntaxe:
Considérons 2 fonctions appelées function1 () et function2 (). Ici, function1 appelle function2 et function2 appelle function1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Exemple
Pour montrer la récursivité indirecte, nous prenons le programme suivant utilisé pour savoir si un nombre donné est pair ou impair à partir de l'entrée donnée.
Code:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Production:
Exemples de récursivité en Java
Voici quelques exemples supplémentaires pour résoudre les problèmes à l'aide de la méthode de récursivité.
Exemple # 1 - séquence de Fibonacci
Un ensemble de «n» nombres serait dans une séquence de Fibonacci si number3 = number1 + number2, c'est-à-dire que chaque nombre est une somme de ses deux nombres précédents. Par conséquent, la séquence commence toujours par les deux premiers chiffres comme 0 et 1. Le troisième chiffre est une somme de 0 et 1 résultant en 1, le quatrième nombre est l'addition de 1 et 1 résultant en 2, et la séquence continue.
Consultez le code suivant en Java pour générer une séquence Fibonacci:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Production:

Ici, les deux premiers nombres sont initialisés à 0 et 1 et imprimés. Les variables «num1», «num2» et «num3» sont utilisées pour générer la séquence requise. La variable «num3» est obtenue en ajoutant «num1» et «num2» et les nombres sont décalés d'une position vers la gauche en mélangeant comme indiqué dans le code. La fonction "Fibonacci" est appelée récursivement ici et à chaque itération, la valeur de "n" est diminuée de 1. D'où la récursivité se termine dès que "n" atteint la valeur 0.
Exemple # 2 - Tour de Hanoi
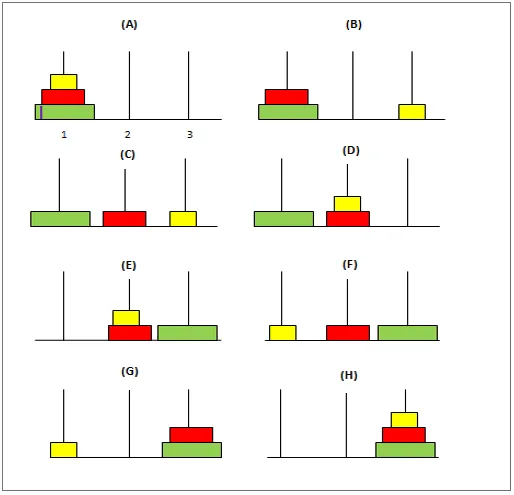
Il s'agit d'un problème mathématique classique qui comporte 3 pôles et un nombre «n» de disques de tailles différentes. Le puzzle se déroule comme suit:
Au début, le premier pôle aura les disques disposés de telle sorte que le plus gros disque de tous se trouve en bas et le plus petit en haut du pôle. L'objectif est de déplacer ces disques du premier pôle au troisième pôle en maintenant les disques dans la même position que celle du premier. Voici quelques conditions à garder à l'esprit lors du déplacement de ces disques:
1. À la fois, un seul disque doit être déplacé.
2. Dans le processus, placer un disque plus grand sur un plus petit n'est pas autorisé.
3. Le deuxième pôle (central) peut être utilisé pour assurer la médiation lors du transfert des disques du premier au deuxième pôle.
Voici le code Java qui peut être utilisé pour résoudre le puzzle:
Code:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Production:
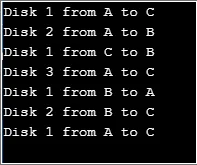
Ici, la variable «count» représente le nombre de disques à utiliser. La fonction «tour» est la fonction récursive utilisée pour déplacer les disques de la tige 1 à la tige 3. Une solution simple à ce problème peut être apportée en considérant 2 disques dans un premier temps.
- Tout d'abord, nous commençons par déplacer le disque 1 de la tige 1 vers la tige 2.
- Ensuite, nous déplaçons disc2 vers la tige 3.
- Enfin, nous terminons en déplaçant le disque 1 sur la tige 3 en complétant la solution requise.
Ce même principe est appliqué pour le nombre "n" de disques en déplaçant (n-1) le disque de la tige 1 à 2 et en suivant des étapes similaires à celles ci-dessus.
Avantages de la récursivité en Java
- Le code est facile à écrire et à maintenir.
- La meilleure méthode pour trouver les résultats où un grand nombre d'itérations est requis.
Inconvénients de la récursivité en Java
- Les fonctions récursives utilisent plus de mémoire. En effet, chaque fois qu'une fonction récursive est appelée; l'allocation de mémoire est effectuée récemment pour les variables de la pile. Et l'allocation de mémoire respective est libérée dès que les valeurs des variables sont retournées.
- Ce processus d'allocation de mémoire prend plus de temps, donc l'exécution est généralement lente.
Conclusion
Les fonctions récursives sont relativement plus simples à coder, mais elles ne sont pas non plus aussi efficaces que les autres méthodes existantes. Par conséquent, ils sont principalement utilisés dans les cas où le temps imparti pour le développement est moindre et où un motif significatif peut être observé dans le problème.
Articles recommandés
Ceci est un guide de la récursivité en Java. Ici, nous discutons des types de récursivité en Java avec ses différents exemples avec les avantages et les inconvénients. Vous pouvez également consulter les articles suivants pour en savoir plus-
- JScrollPane en Java
- Fonctions mathématiques en Java
- Fonctions mathématiques en Java
- Constructeur en Java
- Fonction récursive en Python
- Programme factoriel en JavaScript