
Introduction à la série Fibonacci en Python
Série Fibonacci en Python, c'est ce qu'on appelle une série de nombres, où le nombre suivant est la somme des deux nombres actuels.
Par exemple:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ..so on
Alors ici 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 et ainsi de suite.
En regardant ce qui précède, on aurait eu une certaine idée de ce dont nous parlons.
Cependant, en termes de règle mathématique, cela peut s'écrire:

Où nième nombre est la somme du nombre aux endroits (n-1) et (n-2). En ce qui concerne la mise en œuvre de la série Fibonacci, il pourrait y avoir un certain nombre de langages de codage à travers lesquels cela pourrait être fait.
Cependant, Python est un langage largement utilisé de nos jours. Voyons l'implémentation de la série Fibonacci via Python. Il faut être conscient des instructions de conditionnement de base comme la boucle, if-else, while loop, etc. en Python, avant de procéder ici. Sinon, ce serait bien si on pouvait le réviser et ensuite reprendre le contenu à venir. Ici, à des fins de démonstration, j'utilise spyder qui est IDE pour le langage de programmation python. On peut également utiliser n'importe quel autre bloc-notes IDE ou Ipython pour l'exécution des programmes Python.
Série Fibonacci en Python
Voyons l'implémentation du nombre et de la série de Fibonacci considérant que les deux premiers éléments de Fibonacci sont 0 et 1:
Cependant, vous pouvez modifier la fonction de Fibonacci selon vos besoins, mais voir d'abord les bases et passer progressivement à d'autres.
Code Python pour trouver le nième numéro de Fibonacci
Code 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Code 2:
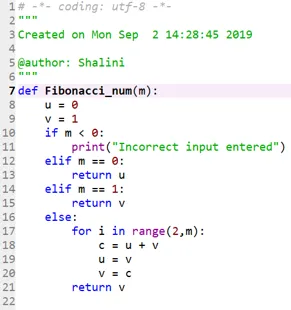
Production:
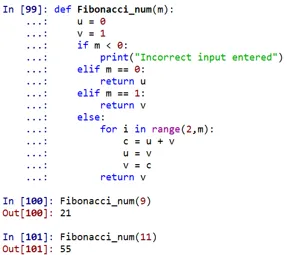
Comme on peut le voir, le nombre de Fibonacci à la 9ème place serait 21 et à la 11ème place serait 55.
- Ici, «fibonacci_num» est une fonction définie, qui s'occupe de trouver le nombre de Fibonacci à l'aide de certaines conditions. Cette fonction peut être appelée en spécifiant n'importe quelle position.
Voyons maintenant comment imprimer des séries jusqu'à la position mentionnée:
Code:
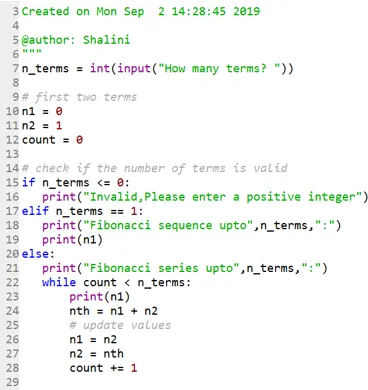
Production:
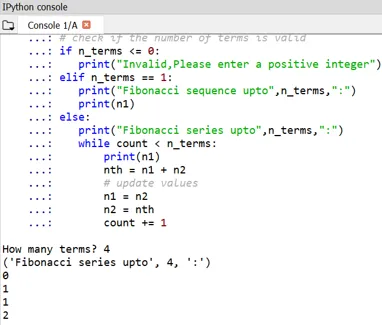
On peut remarquer que le début des nombres de Fibonacci est défini comme 0 et 1.
- Si quelqu'un veut définir ses propres termes de départ, cela peut également être fait de la même manière en peaufinant n1 et n2. Voici l'exemple pour cela:
Disons maintenant que nous voulons que nos termes de départ soient: n1 = 3, n2 = 5
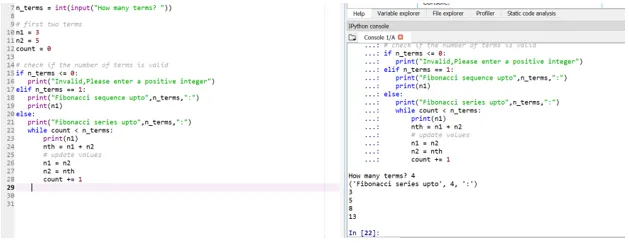
Donc, ici, votre position au 4 e terme (la saisie de l'utilisateur est prise), sera décidée en fonction de vos conditions de départ.
Méthodes par lesquelles la série Fibonacci peut être générée
Voici les trois méthodes, grâce auxquelles les séries de Fibonacci peuvent être générées:
1. Grâce à des générateurs
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Production:
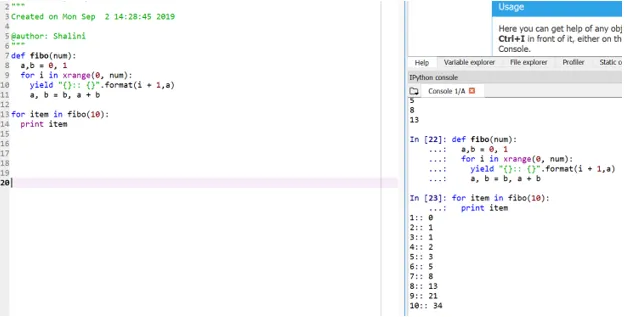
Cette méthode est appelée «générateur» car la fonction xrange est un générateur de nombres compris entre 0 et num et le rendement est le générateur de sortie formatée.
Voici ce que xrange fait pour vous:

Ici, la série de Fibonacci a été définie sous la forme d'une fonction, à l'intérieur de laquelle la fonction boucle, xrange et yield prend en charge la sortie.
2. À travers pour la boucle
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Production:

Comme on peut le voir, une boucle simple a été utilisée pour imprimer la série de Fibonacci entre 0 et 10. À l'intérieur de la boucle, de nouvelles valeurs ont été affectées aux variables. U et v sont les valeurs initiales par défaut de Fibonacci qui ont été définies respectivement sur 0 et 1.
Au fur et à mesure que la boucle progresse, la nouvelle valeur u est l'ancienne valeur v, tandis que la nouvelle valeur v est la somme des anciennes valeurs de u et v. Cela continue jusqu'à la fin des valeurs de plage.
3. Par récursivité
Code:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Production:
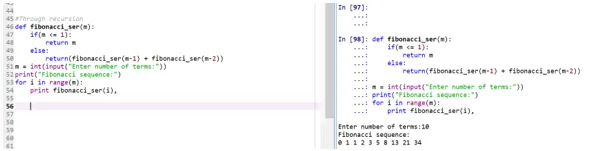
- La fonction "fibonacci_ser" se lance un appel pour imprimer la série Fibonacci.
- Et donc la méthode a son nom de «récursivité».
Étapes suivies ici:
- Ici, l'utilisateur a été invité à entrer le lieu jusqu'à lequel la série Fibonacci doit être imprimée.
- Le nombre passe par la fonction "fibonacci_ser".
- La condition est vérifiée, si la longueur fournie est inférieure à 1 ou non. Si oui, le résultat est donné immédiatement.
- Cependant, si la longueur est supérieure à 1, des appels récursifs sont effectués vers «fibonacci_ser» avec des arguments de longueur inférieure à 1 et 2, c'est-à-dire fibonacci_ser (m-1) et fibonacci_ser (m-2).
- Par conséquent, la récursivité donne la sortie souhaitée et l'imprime.
- Donc, en bref, nous avons discuté de trois façons d'afficher la série Fibonacci.
- À travers la boucle, les générateurs et la récursivité.
Résumé des trois codes Python
Voici les trois codes python:
1. Grâce à des générateurs
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. À travers pour la boucle
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Par récursivité
Code:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Toutes les procédures sont résumées ci-dessus, il faut s'entraîner pour bien saisir tout le monde.
Production:
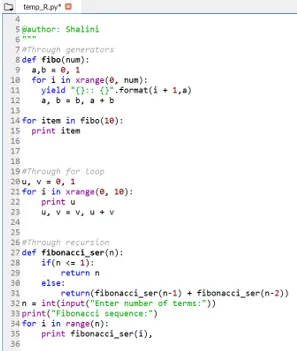
Conclusion
En parcourant le contenu ci-dessus de Fibonacci, on aurait eu une compréhension limpide des nombres et des séries de Fibonacci, spécialisée dans le python. Une fois, on se familiarise avec la logique de la série Fibonacci, générer un autre ensemble de séries, travailler avec d'autres numéros et avec différentes méthodes sera désormais un gâteau pour vous. Une approche logique est le seul moyen d'exceller dans ce domaine.
Articles recommandés
Ceci est un guide de la série Fibonacci en Python. Nous discutons ici des nombres et des séries de Fibonacci, spécialisés avec python, générant un autre ensemble de séries, travaillant avec d'autres nombres et avec diverses méthodes. Vous pouvez également consulter nos autres articles connexes pour en savoir plus -
- Générateur de nombres aléatoires en Python
- Fonctions mathématiques en Python
- Factorial en Python
- Encapsulation en Python
- Série Fibonacci en Java
- Fonctionnalités de Python
- Programme factoriel en JavaScript
- Générateur de nombres aléatoires dans Matlab
- Générateur de nombres aléatoires en C #
- Encapsulation en JavaScript