
Introduction au tri par fusion en JavaScript
Les algorithmes de tri sont très importants en informatique. Le résultat du tri consiste à organiser les éléments d'une liste dans un certain ordre (croissant ou décroissant). Merge Sort en JavaScript est l'un des algorithmes de tri les plus efficaces disponibles car il est basé sur le concept de division et de conquête. Comme son nom l'indique, divisez d'abord le plus gros problème en petits problèmes plutôt que de résoudre les petits problèmes afin de résoudre le plus gros problème. Conceptuellement, le tri par fusion est une combinaison de deux algorithmes de base appelés MERGE et MERGE_SORT.
qui fonctionne comme suit:
- Divisez la liste non triée en n nombre de sous-listes d'éléments uniques (n est le nombre total d'éléments dans la liste non triée).
- Fusionner à plusieurs reprises les sous-listes en sous-listes triées jusqu'à ce qu'il n'y ait qu'une seule liste triée.
Implémentation du tri par fusion en JavaScript
L'algorithme MERGE suit la procédure de combinaison de deux listes triées en une seule liste triée.
Exemple: Supposons qu'il existe deux listes, à savoir la liste 1 (1, 5, 3) et la liste 2 (7, 2, 9).
1. Triez d'abord les deux listes.
Maintenant, nous allons voir et appliquer la technique E dessus.
2. Ensuite, nous allons créer une nouvelle liste de taille x + y où x est le nombre d'éléments dans la liste 1 et y est le nombre d'éléments dans la liste 2.

Dans notre cas, x = 3 et y = 3, donc x + y = 6.
3. Maintenant, nous avons deux pointeurs.
Un premier pointeur pointant vers la première position de la liste 1 et un second pointeur pointant vers la première position de la liste 2.

4. Ensuite, nous comparerons la valeur des deux pointeurs. Le pointeur avec une valeur moindre, copiez cet élément dans la liste 3 et déplacez le pointeur vers la droite de la liste avec une valeur plus petite et la liste résultante (c'est-à-dire la liste 1 et la liste 3)

5. De même, répétez l'étape 4 encore et encore.

Traverser plus loin… ..
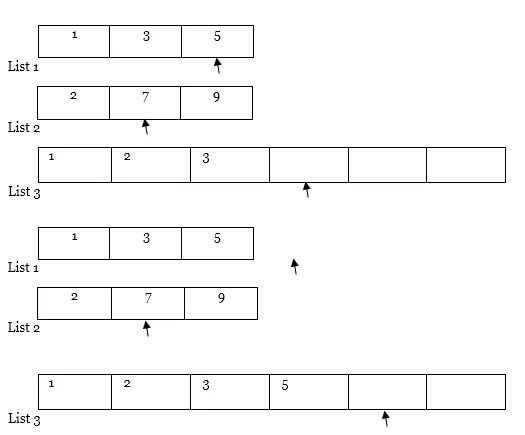
Remarque : Si l'une des listes (c'est-à-dire la liste 1 ou la liste 2) est entièrement parcourue comme dans le cas, copiez le contenu entier d'une autre liste du pointeur vers la liste des résultats (c'est-à-dire la liste 3) comme suit.

Pseudocode
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
L'algorithme MERGE_SORT divise la liste non triée donnée en taille minimale, puis appelle l'algorithme MERGE pour combiner la liste dans la nouvelle liste triée.
Pseudocode
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Exemple
Ici, nous suivons l'implémentation descendante du tri par fusion. Il commence en haut et se poursuit vers le bas, chaque tour récursif posant la même question «Que faut-il faire pour trier la liste?» Et ayant la réponse «Diviser la liste en deux, effectuer un appel récursif et fusionner le résultats".
Code en Javascript
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
La fonction principale du tri par fusion divisera la liste donnée en listes plus petites à chaque itération de l'appel récursif. N'oubliez pas que la récursivité nécessite la condition de base afin d'éviter une récursion infinie. Dans notre cas, nous avons:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Après avoir configuré la condition de base pour la récursivité, nous identifierons ensuite l'index du milieu pour diviser la liste donnée en sous-liste gauche et droite, comme vous pouvez le voir ci-dessus dans le diagramme d'exemple. Ensuite, nous devons fusionner la sous-liste de gauche et la sous-liste de droite que nous allons examiner maintenant. Dans la fonction de fusion ci-dessus, nous devons nous assurer que nous trions tous les éléments de la sous-liste de gauche et de la sous-liste de droite. liste. Pour ce faire, nous utilisons une boucle while. Dans la boucle while, nous comparerons un par un l'élément de la sous-liste de gauche et l'élément de la sous-liste de droite. Nous pouvons pousser le plus petit des deux dans la liste des résultats et déplacer le curseur de la sous-liste de gauche et de la sous-liste de droite en conséquence. Enfin, nous devons concaténer la liste des résultats. C'est très important! Si nous ne faisons pas cette dernière étape ici, nous aurons une liste d'éléments incomplète à la fin parce que la condition de boucle while échouera une fois que l'un des deux pointeurs atteindra la fin.
Production:

Propriétés du tri par fusion
- Le tri par fusion est stable car le même élément d'un tableau conserve sa position d'origine les uns par rapport aux autres.
- Le tri par fusion n'est pas «en place» car lors de la fusion, il crée une copie de la liste entière qui est triée. Pour cette raison, la complexité spatiale (O (n)) de cet algorithme est en fait plus grande que d'autres, et ne doit pas être utilisée dans des problèmes complexes où l'espace est premium.
- La complexité temporelle globale du tri par fusion est O (nLogn). Il est plus efficace car dans le pire des cas également, le runtime est O (nlogn).
Conclusion
Les complexités temporelles du meilleur, du pire et du cas moyen de fusion sont les mêmes, ce qui en fait un algorithme plus efficace. Il fonctionne plus rapidement que les autres techniques de tri. Le tri par fusion peut être appliqué à des fichiers de toute taille. Il est hautement parallélisable en raison de l'utilisation de la méthode diviser pour régner. Afin de développer des bases solides en informatique, il est conseillé de bien comprendre les différents algorithmes de tri.
Article recommandé
Cela a été un guide pour fusionner le tri en JavaScript. Nous discutons ici de l'introduction au tri par fusion en JavaScript et de l'implémentation ainsi que des propriétés. Vous pouvez également consulter nos autres articles suggérés pour en savoir plus -
- Fonctions mathématiques JavaScript
- Introduction à JavaScript
- Meilleurs cadres Javascript
- Outils JavaScript
- Top 6 des algorithmes de tri en JavaScript