Formule de composition continue - Calculatrice (modèle Excel)

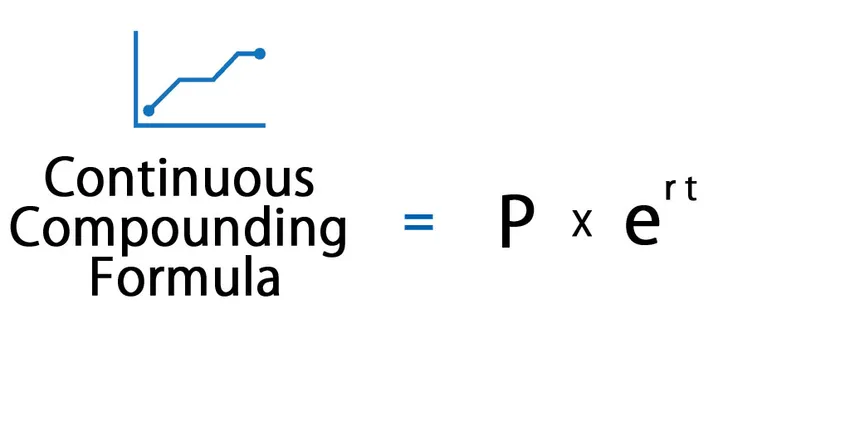
Formule composée continue (Table des matières)

• Formule de composition continue
• Calculatrice de composition continue
• Formule de composition continue dans Excel (avec modèle Excel)

Formule de composition continue

Avant de passer au concept de composition continue, comprenons d'abord ce qu'est l'intérêt composé. L'intérêt composé signifie que les intérêts que les investisseurs gagnent chaque année s'ajoutent à son capital, de sorte que le montant ne fait pas que croître, il augmente à un taux plus élevé que le simple taux d'intérêt - est l'un des concepts les plus utiles en finance. Il est à la base de tout, d'un plan d'investissement à long terme sur le marché des actions au plan d'épargne personnel. Il prend également en compte les effets de l'inflation sur le montant et l'importance de payer la detteFormule de ratio de frais généraux | Calculatrice (modèle Excel).

Pour une composition continue, le taux d'intérêt est ajouté à chaque instant. Cela rend le calcul difficile. Ce montant n'est utilisé par aucune institution financière pour les frais d'intérêt, car il y a peu de différence entre le montant composé en continu et le montant composé quotidiennement. Les banques utilisent quotidiennement le montant des intérêts composés dans certains de leurs produits.

La formule de composition continue est la suivante:

La formule de composition continue calcule les intérêts gagnés qui sont composés en continu pendant une période de temps infinie.

où,

P = Montant principal (Valeur actuelle du montant)

t = temps (le temps est en années)

r = taux d'intérêt.

Le calcul ci-dessus suppose un intérêt composé constant sur une période de temps infinie. La période mentionnée étant infinie, la fonction exposant (e) contribue à une multiplication du montant d'investissement actuel. Il est multiplié par le taux d'intérêt actuel et la période. Malgré un grand nombre d'investissements, la différence entre le total des intérêts gagnés grâce à la composition continue d'Excel est la même que celle des intérêts composés traditionnels.

Exemples et explication de la formule de composition continue

Calculez l'intérêt composé sur le capital de 10 000 $ avec un taux d' intérêt de 8% et une période de 1 an. La fréquence de composition est un composé semestriel, semestriel, trimestriel, mensuel et continu.

Vous pouvez télécharger ce modèle de composition continue ici - Modèle de composition continue

Valeur future composée annuelle:

• Valeur future = 10 000 * (1 + 0, 08) 1
• Valeur future = 10 800 $

Valeur future composée semestrielle:

• Valeur future = 10 000 * ((1 + 0, 08 / 2)) 2
• Valeur future = 10 000 * (1, 04) 2
• Valeur future = 10 000 * 1, 0816
• Valeur future = 10 816, 0 $

Valeur future composée trimestrielle:

• Valeur future = 10 000 * ((1 + 0, 08 / 4)) 4
• Valeur future = 10 000 * (1, 02) 4
• Valeur future = 10 000 * 1, 08243
• Valeur future = 10 824, 3 $

Valeur future composée mensuelle:

• Valeur future = 10000 * ((1 + 0, 08 / 12)) 12
• Valeur future = 10 000 * (1, 006) 4
• Valeur future = 10 000 * 1, 083
• Valeur future = 10 830 $

Valeur future composée continue:

• Valeur future = 10 000 * e ^{0, 08}
• Valeur future = 10 000 * 1, 08328
• Valeur future = 10 832, 87 $

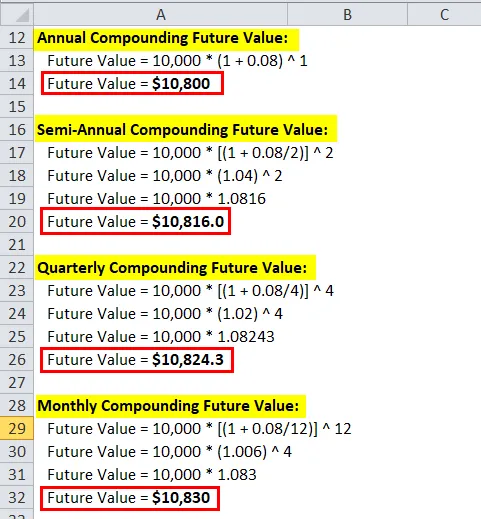
Comme le montre l'exemple ci-dessus de calculs de composition avec différentes fréquences, l'intérêt calculé à partir d'une composition continue est de 832, 9 $, ce qui ne représente que 2, 9 $ de plus que la composition mensuelle. Il est donc nécessaire d'utiliser le taux d'intérêt composé mensuel ou quotidien dans la vie pratique que le taux d'intérêt composé continu.

Importance et utilisation de la formule composée continue

L'importance de la formule de composition continue est:

• Au lieu d'une composition continue des intérêts sur une base annuelle, trimestrielle ou mensuelle, la combinaison continue d'Excel réinvestira efficacement les gains au fil du temps.
• L'effet composé continu permet de réinvestir continuellement le montant des intérêts au même taux d'intérêt, donnant ainsi à l'investisseur la possibilité de générer des rendements à un taux exponentiel.
• La composition continue détermine que ce n'est pas seulement le montant principal qui rapportera de l'argent, mais aussi la composition continue du montant d'intérêt continuera également à multiplier le montant.

La composition peut être effectuée sur une base annuelle, semestrielle, trimestrielle, quotidienne ou continue. La différence entre ces périodes est qu'après avoir terminé la période, tout intérêt gagné est traité comme un nouveau principal. Par exemple, si la fréquence de composition est semestrielle, des intérêts seront ajoutés au capital après six mois, ce cycle se poursuit jusqu'à l'échéance. Il en va de même pour une autre période: pour les intérêts annuels s'ajoutant après un an, pour les intérêts trimestriels s'ajoutant après trois mois, pour les intérêts quotidiens s'ajoutant le lendemain.

Calculatrice de composition continue

Vous pouvez utiliser la calculatrice de composition continue suivante

P
r
t
Formule de composition continue =

Formule de composition continue =	P xe (rxt)
=	0 xe (0 x 0) = 0

Formule de composition continue dans Excel (avec modèle Excel)

Ici, nous ferons le même exemple de la formule de composition continue dans Excel. C'est très facile et simple. Vous devez fournir les trois entrées, à savoir le montant principal, le taux d'intérêt et le temps.

Vous pouvez facilement calculer la composition continue à l'aide de la formule dans le modèle fourni.

Tout d'abord, nous devons calculer le montant de composition continue à l'aide de la formule

ensuite, nous devons calculer les effets de la même chose sur la composition régulière:

Articles recommandés

Cela a été un guide pour une formule de composition continue. Ici, nous discutons de ses utilisations ainsi que des exemples pratiques. Nous vous fournissons également une calculatrice de composition continue avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -

1. Crédit d'impôt vs déduction fiscale - Comparaison
2. Différence entre le taux d'intérêt simple et le taux d'intérêt composé
3. Taux d'actualisation vs taux d'intérêt - principales différences
4. Meilleures techniques pour les meilleurs prospects en ligne