Introduction aux algorithmes de tri par fusion en Java
Les algorithmes de tri par fusion sont très importants en informatique. Le résultat du tri est d'organiser les éléments d'une liste dans un certain ordre (croissant ou décroissant). Le tri par fusion est l'un des algorithmes de tri les plus efficaces disponibles car il est basé sur le concept de division et de conquête. Comme son nom l'indique, divisez d'abord le plus gros problème en petits problèmes plutôt que de résoudre les petits problèmes afin de résoudre le plus gros problème. Dans cet article, nous discuterons des algorithmes de tri de fusion en Java. Conceptuellement, le tri par fusion est une combinaison de deux algorithmes de base appelés MERGE et MERGE_SORT qui fonctionnent comme suit:
- Divisez la liste non triée en n nombre de sous-listes d'éléments uniques (n est le nombre total d'éléments dans la liste non triée).
- Fusionner à plusieurs reprises les sous-listes en sous-listes triées jusqu'à ce qu'il n'y ait qu'une seule liste triée.
Implémentation d'algorithmes de tri par fusion en Java
L'algorithme MERGE est la procédure de combinaison de deux listes triées en une seule liste triée.
Exemple: Supposons qu'il existe deux listes, à savoir la liste 1 (6, 3) et la liste 2 (3, 1, 9).
1. Triez d'abord les deux listes.
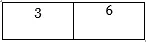
Liste 1

Liste 2
Maintenant, nous allons y appliquer une technique de fusion.
- Ensuite, nous allons créer une nouvelle liste de taille m + n où m est le nombre d'éléments dans la liste 1 et n est le nombre d'éléments dans la liste 2.

Liste 3
Dans notre cas, m = 2 et n = 3, donc m + n = 5.
- Maintenant, nous avons un pointeur à deux points. Un premier pointeur pointant vers la première position de la liste 1 et un second pointeur pointant vers la première position de la liste 2.
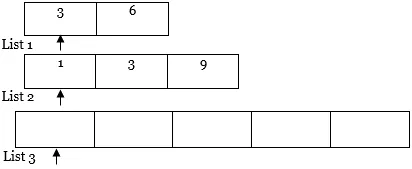
4. Ensuite, nous comparerons la valeur des deux pointeurs. Le pointeur avec une valeur moindre, copiez cet élément dans la liste 3 et déplacez le pointeur vers la droite de la liste avec une valeur plus petite et la liste résultante (c'est-à-dire la liste 1 et la liste 3).
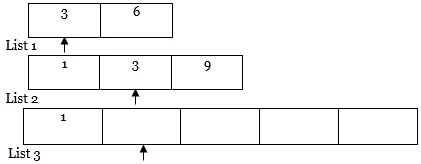
5. De même, répétez l'étape 4 encore et encore.
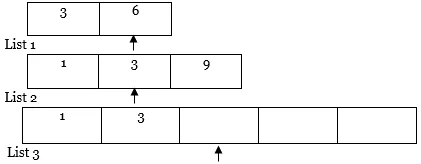
Traverser plus loin… ..
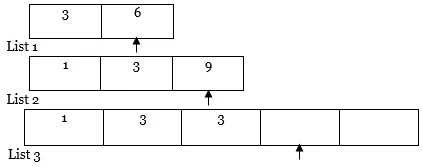
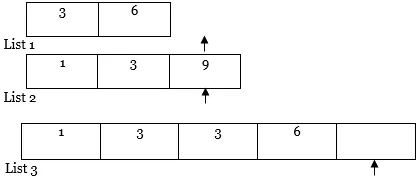
REMARQUE: Si l'une des listes (c'est-à-dire la liste 1 ou la liste 2) est entièrement parcourue comme dans le cas ci-dessus, copiez le contenu entier des autres listes du pointeur vers la liste des résultats (c'est-à-dire la liste 3) comme suit.

Algorithme et pseudocode
Les deux algorithmes utilisés dans l'algorithme de fusion sont:
- Le MERGE (ARR, F, M, L) est un processus qui suppose ce qui suit:
- ARR (F… .M) et ARR (M + 1… .L) sont des listes triées.
- Fusionne les deux sous-listes triées en un seul ARR (F… .L).
- SORT (ARR (), F, L) // ici F est le premier et L est le dernier index du tableau.
Si (L> 1)
- Trouvez le point central pour diviser la liste en deux moitiés:
milieu M = (F + L) / 2
- Tri par fusion d'appels pour le premier semestre:
Appelez SORT (ARR, 1, M)
- Appel Merge Sort pour la seconde moitié:
Appelez SORT (ARR, M + 1, L)
- Fusionnez les moitiés triées aux étapes 2 et 3:
Appeler MERGE (ARR, L, M, R)
Exemple
Prenons un exemple de tableau ARR (10, 6, 8, 5, 7, 3, 4). Nous utiliserons l'algorithme de fusion pour trier le tableau à l'aide de sa technique de division et de conquête. Nous pouvons voir la figure ci-dessous que le tableau est récursivement divisé en deux moitiés jusqu'à ce que la taille devienne 1. Une fois que la taille devient 1, nous appelons les processus de fusion et recommençons à fusionner les listes jusqu'à ce que la liste complète soit fusionnée.
REMARQUE: dans la figure ci-dessous, les chiffres en rouge indiquent l'ordre dans lequel les étapes sont traitées pour former le tableau trié.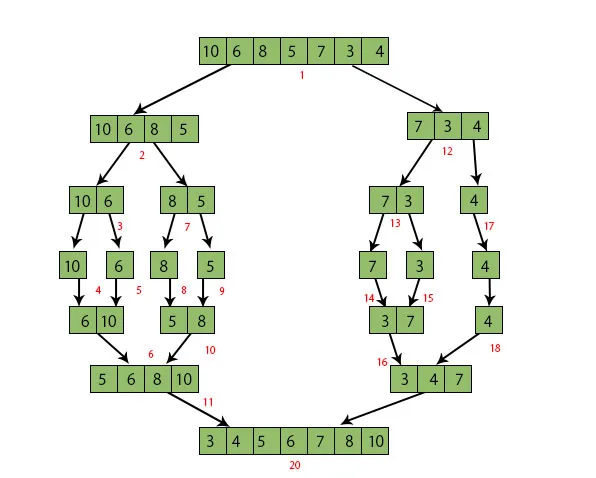
Code du programme:
import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)
Production:
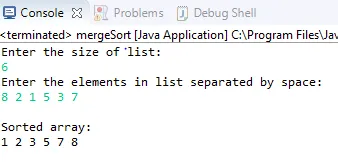
Conclusion - Fusionner les algorithmes de tri en Java
Les complexités temporelles du meilleur, du pire et du cas moyen de fusion sont les mêmes, ce qui en fait un algorithme plus efficace. Il fonctionne plus rapidement que les autres techniques de tri. Le tri par fusion peut être appliqué à des fichiers de toute taille. Il est hautement parallélisable en raison de l'utilisation de la méthode diviser pour régner. Afin de développer des bases solides en informatique, il est conseillé de bien comprendre les différents algorithmes de tri.
Articles recommandés
Ceci est un guide des algorithmes de tri de fusion en Java. Nous discutons ici de la mise en œuvre d'algorithmes de tri de fusion en java et d'algorithme et de pseudocode avec un exemple. Vous pouvez également consulter nos autres articles suggérés -
- Tri de sélection en Java
- Déclaration de cas en Java
- Modificateurs d'accès en Java
- Fusionner le tri en JavaScript
- Qu'est-ce que la déclaration de cas en JavaScript?
- Modificateurs d'accès en PHP
- Algorithmes de tri rapide en Java
- Guide complet de tri en C # avec des exemples
- Fonction de tri en Python avec des exemples
- Top 6 des algorithmes de tri en JavaScript