
Formule de marge d'erreur (Table des matières)
- Formule de marge d'erreur
- Exemples de formule de marge d'erreur (avec modèle Excel)
- Calculatrice de marge d'erreur
Formule de marge d'erreur
En statistique, nous calculons l'intervalle de confiance pour voir où la valeur des données de l'échantillon statistique tombera. La plage de valeurs inférieures et supérieures à la statistique d'échantillon dans un intervalle de confiance est appelée marge d'erreur. En d'autres termes, il s'agit essentiellement du degré d'erreur dans l'échantillon statistique. Plus la marge d'erreur est élevée, moins la confiance dans les résultats sera grande car le degré de déviation de ces résultats est très élevé. Comme son nom l'indique, la marge d'erreur est une plage de valeurs au-dessus et au-dessous des résultats réels. Par exemple, si nous obtenons une réponse dans une enquête dans laquelle 70% des personnes ont répondu «bien» et la marge d'erreur est de 5%, cela signifie qu'en général, 65% à 75% de la population pense que la réponse est «bonne» .
La formule de la marge d'erreur -
Margin of Error = Z * S / √n
Où:
- Score Z - Z
- S - Écart type d'une population
- n - Taille de l'échantillon
Une autre formule pour calculer la marge d'erreur est:
Margin of Error = Z * √((p * (1 – p)) / n)
Où:
- p - Proportion d'échantillon (fraction de l'échantillon qui est un succès)
Maintenant, pour trouver le score z souhaité, vous devez connaître l'intervalle de confiance de l'échantillon car le score Z en dépend. Le tableau ci-dessous est donné pour voir la relation d'un intervalle de confiance et d'un score z:
| Intervalle de confiance | Z - Score |
| 80% | 1, 28 |
| 85% | 1, 44 |
| 90% | 1, 65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Une fois que vous connaissez l'intervalle de confiance, vous pouvez utiliser la valeur z correspondante et calculer la marge d'erreur à partir de là.
Exemples de formule de marge d'erreur (avec modèle Excel)
Prenons un exemple pour mieux comprendre le calcul de la marge d'erreur.
Vous pouvez télécharger ce modèle de marge d'erreur ici - Modèle de marge d'erreurFormule de marge d'erreur - Exemple # 1
Disons que nous menons une enquête pour voir quel est le score obtenu par les étudiants universitaires. Nous avons sélectionné 500 élèves au hasard et demandé leur note. La moyenne est de 2, 4 sur 4 et l'écart type est de 30%. Supposons que l'intervalle de confiance est de 99%. Calculez la marge d'erreur.
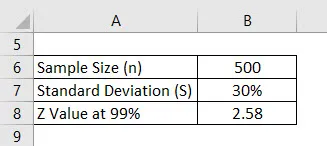
Solution:
La marge d'erreur est calculée à l'aide de la formule ci-dessous
Marge d'erreur = Z * S / √n
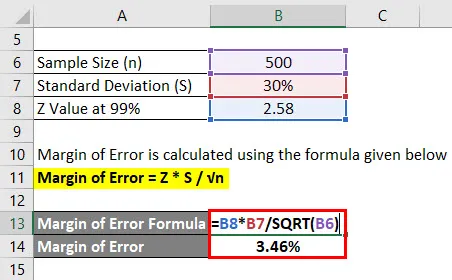
- Marge d'erreur = 2, 58 * 30% / √ (500)
- Marge d'erreur = 3, 46%
Cela signifie qu'avec une confiance de 99%, la note moyenne des élèves est de 2, 4 plus ou moins 3, 46%.
Formule de marge d'erreur - Exemple # 2
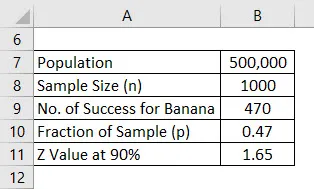
Disons que vous lancez un nouveau produit de santé sur le marché, mais vous ne savez pas quelle saveur plaira aux gens. Vous êtes confus entre la saveur de banane et la saveur de vanille et avez décidé de mener une enquête. Votre population pour cela est de 500 000 qui est votre marché cible et à partir de cela, vous avez décidé de demander l'avis de 1000 personnes et ce sera l'échantillon. Supposons qu'un intervalle de confiance est de 90%. Calculez la marge d'erreur.
Solution:
Une fois l'enquête terminée, vous avez appris que 470 personnes ont aimé la saveur de banane et 530 ont demandé la saveur de vanille.
La marge d'erreur est calculée à l'aide de la formule ci-dessous
Marge d'erreur = Z * √ ((p * (1 - p)) / n)
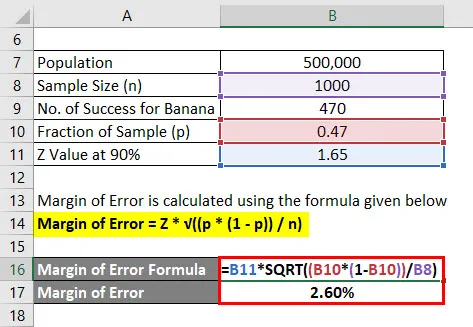
- Marge d'erreur = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Marge d'erreur = 2, 60%
Nous pouvons donc dire qu'avec 90% de confiance, 47% de toutes les personnes ont aimé la saveur de banane plus ou moins 2, 60%.
Explication
Comme indiqué ci-dessus, la marge d'erreur nous aide à comprendre si la taille de l'échantillon de votre enquête est appropriée ou non. Dans le cas où l'erreur de marge est trop importante, il peut arriver que notre taille d'échantillon soit trop petite et nous devons l'augmenter pour que les résultats de l'échantillon correspondent plus étroitement aux résultats de la population.
Il existe certains scénarios où la marge d'erreur ne sera pas très utile et ne nous aidera pas à suivre l'erreur:
- Si les questions de l'enquête ne sont pas conçues et ne permettent pas d'obtenir la réponse requise
- Si les personnes qui répondent à l'enquête ont un certain biais concernant le produit pour lequel l'enquête est effectuée, alors aussi, le résultat n'est pas très précis
- Si l'échantillon choisi lui-même est le bon représentant de la population, dans ce cas également, les résultats seront très éloignés.
En outre, une grande hypothèse ici est que la population est normalement distribuée. Donc, si la taille de l'échantillon est trop petite et la distribution de la population n'est pas normale, le score z ne peut pas être calculé et nous ne serons pas en mesure de trouver la marge d'erreur.
Pertinence et utilisations de la formule de la marge d'erreur
Chaque fois que nous utilisons des échantillons de données pour trouver une réponse pertinente pour l'ensemble de la population, il y a une certaine incertitude et des chances que le résultat s'écarte du résultat réel. La marge d'erreur nous dira que quel est le niveau de déviation s'il y a la sortie de l'échantillon. Nous devons minimiser la marge d'erreur afin que nos résultats d'échantillonnage décrivent l'histoire réelle des données de population. Donc, abaissez la marge d'erreur, meilleurs seront les résultats. La marge d'erreur complète et complète les informations statistiques dont nous disposons. Par exemple, si un sondage révèle que 48% des gens préfèrent passer du temps à la maison pendant le week-end, nous ne pouvons pas être aussi précis et il y a des éléments manquants dans cette information. Lorsque nous avons introduit une marge d'erreur ici, disons, 5%, le résultat sera interprété comme 43 à 53% des gens ont aimé l'idée d'être à la maison pendant le week-end, ce qui est tout à fait logique.
Calculatrice de marge d'erreur
Vous pouvez utiliser la calculatrice de marge d'erreur suivante
| Z | |
| S | |
| √n | |
| Marge d'erreur | |
| Marge d'erreur | = |
|
|
Articles recommandés
Cela a été un guide pour la formule de la marge d'erreur. Nous discutons ici comment calculer la marge d'erreur ainsi que des exemples pratiques. Nous fournissons également une calculatrice de marge d'erreur avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Guide de la formule d'amortissement linéaire
- Exemples de formule de temps de doublement
- Comment calculer l'amortissement?
- Formule pour le théorème de limite centrale
- Altman Z Score | Définition | Exemples
- Formule d'amortissement | Exemples avec modèle Excel