
Formule de score Z (Table des matières)
- Formule
- Exemples
- Calculatrice
Qu'est-ce que la formule de score Z?
Le «score Z» est l'un des outils statistiques les plus utilisés pour normaliser le score, à condition que les moyennes de population et l'écart type soient connus. En tant que tel, le score Z est également connu comme le score standard. Le score Z varie de -3 fois l'écart-type à +3 fois l'écart-type avec une moyenne de zéro et un écart-type de un. La formule du score Z d'une variable peut être dérivée en déduisant la moyenne de la population de la variable donnée (qui fait partie de l'ensemble de données ou de la population), puis en divisant le résultat par l'écart-type de la population. Mathématiquement, il est représenté comme,
Z = (X – μ) / σ
où,
- X = Variable de la population
- μ = Moyenne de la population
- σ = écart type de la population
Exemples de formule de score Z (avec modèle Excel)
Prenons un exemple pour mieux comprendre le calcul du score Z.
Vous pouvez télécharger ce modèle Excel de formule de score Z ici - Modèle Excel de formule de score ZFormule de score Z - Exemple # 1
Prenons l'exemple de Manny qui a récemment comparu pour SAT. Il a réussi à marquer 1109 dans cette tentative. Cependant, selon les informations disponibles, le score moyen pour SAT est resté autour de 1030 avec un écart-type de 250. Calculez le score Z pour le score SAT de Manny et évaluez ses performances par rapport aux candidats moyens.
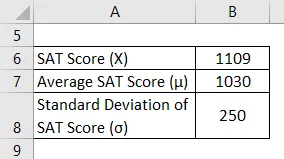
Solution:
Le score Z est calculé à l'aide de la formule ci-dessous
Z = (X - μ) / σ
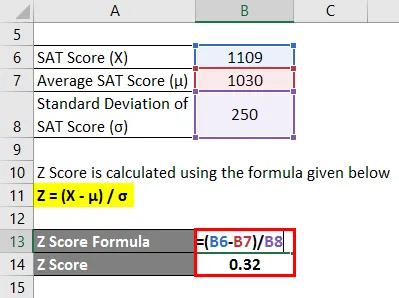
- Score Z = (1109 - 1030) / 250
- Score Z = 0, 32
Par conséquent, le score SAT de Manny est de 0, 32 écart-type supérieur au score moyen des candidats, ce qui indique que 62, 55% des candidats ont obtenu un score inférieur à Manny.
Formule de score Z - Exemple # 2
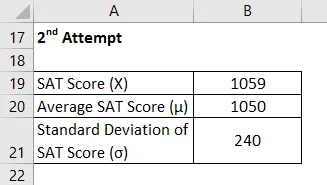
Maintenant, prenons l'exemple de Chelsea qui a écrit deux fois la SAT et veut comparer sa performance en eux. Elle a réussi à marquer 1085 et 1059 dans ses 1 er et 2 e tentatives respectivement. Selon les informations disponibles, le score moyen et l'écart type au cours de la 1ère tentative étaient respectivement de 1100 et 230, alors que dans ce dernier il était de 1050 et 240 respectivement. Veuillez aider Chelsea à décider à quel examen elle a obtenu les meilleurs résultats.
Solution:
1 ère tentative
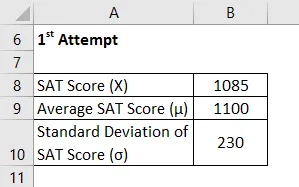
Le score Z est calculé à l'aide de la formule ci-dessous
Z = (X - μ) / σ
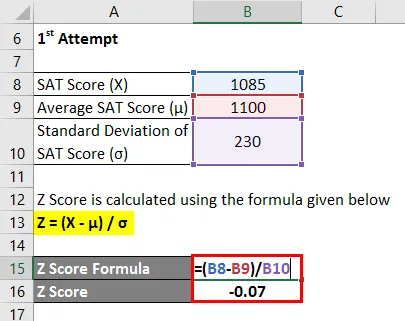
- Score Z = (1085 - 1100) / 230
- Score Z = -0, 07
Par conséquent, le score SAT de Chelsea lors de la première tentative est de 0, 07 écart-type inférieur au score moyen des candidats, ce qui indique que 47, 40% des candidats ont obtenu un score inférieur à Chelsea lors de la première tentative.
2 e tentative
Le score Z est calculé à l'aide de la formule ci-dessous
Z = (X - μ) / σ
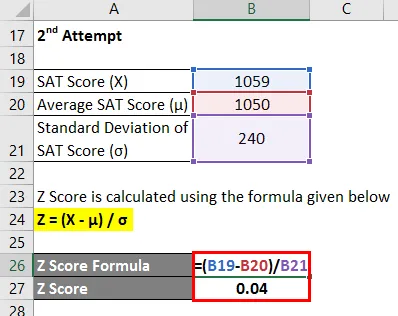
- Score Z = (1059 - 1050) / 240
- Score Z = 0, 04
Par conséquent, le score SAT de Chelsea lors de la 2 e tentative est supérieur de 0, 04 écart-type au score moyen des candidats, ce qui indique que 51, 50% des candidats ont obtenu moins que Chelsea lors de la 2 e tentative.
Ainsi, à partir de la comparaison des scores Z, il est clair que Chelsea a mieux performé lors de sa 2 ème tentative.
Explication
La formule du score Z peut être dérivée en utilisant les étapes suivantes:
Étape 1: Premièrement, construisez une population avec un grand nombre de variables et les variables sont désignées par X i .
Étape 2: Ensuite, le nombre de variables dans la population est calculé et il est noté N.
Étape 3: Ensuite, la moyenne de la population est calculée en additionnant toutes les variables suivies d'une division par le nombre total de variables (étape 2) dans l'ensemble de données. La moyenne de la population est notée μ.
μ = ∑ X i / N
Étape 4: Ensuite, déduisez la moyenne de chaque variable de l'ensemble de données pour calculer leur écart par rapport à la moyenne.
c'est-à-dire que (X i - μ) est l'écart pour le i ème point de données.
Étape 5: Ensuite, calculez les écarts au carré pour les variables, c'est-à-dire (X i - μ) 2 .
Étape 6: Ensuite, additionnez tous les écarts au carré, puis divisez le total par le nombre de variables dans l'ensemble de données pour arriver à la variance.
σ 2 = ∑ (X i - μ) 2 / N
Étape 7: Ensuite, l'écart-type de la population est calculé en calculant la racine carrée de la variance calculée à l'étape ci-dessus.
σ = √ ∑ (X i - μ) 2 / N
Étape 8: Enfin, la formule du score Z est dérivée en déduisant la moyenne de la population (étape 3) de la variable, puis en divisant le résultat par l'écart-type de la population (étape 7) comme indiqué ci-dessous.
Z = (X - μ) / σ
Pertinence et utilisations de la formule du score Z
Du point de vue d'un statisticien, le concept de score Z est très important car il est utile pour déterminer la probabilité qu'un événement se produise ou non dans une distribution normale. En fait, le score Z est également utilisé pour comparer deux scores bruts de deux distributions normales différentes et cela se fait en convertissant les scores bruts en score Z ou score standardisé. De plus, un score Z positif implique un score supérieur à la moyenne, tandis qu'un score Z négatif implique un score inférieur à la moyenne.
Calculateur de formule de score Z
Vous pouvez utiliser le calculateur de formule de score Z suivant
| X | |
| µ | |
| σ | |
| Z | |
| Z = |
|
|
Articles recommandés
Cela a été un guide pour la formule de score Z. Nous discutons ici comment calculer le score Z avec des exemples pratiques. Nous fournissons également un calculateur de score Z avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Exemples de formule de taille d'échantillon
- Comment calculer la moyenne pondérée?
- Calculatrice pour la formule de corrélation
- Formule pour calculer la distribution normale
- Exemples de score Altman Z