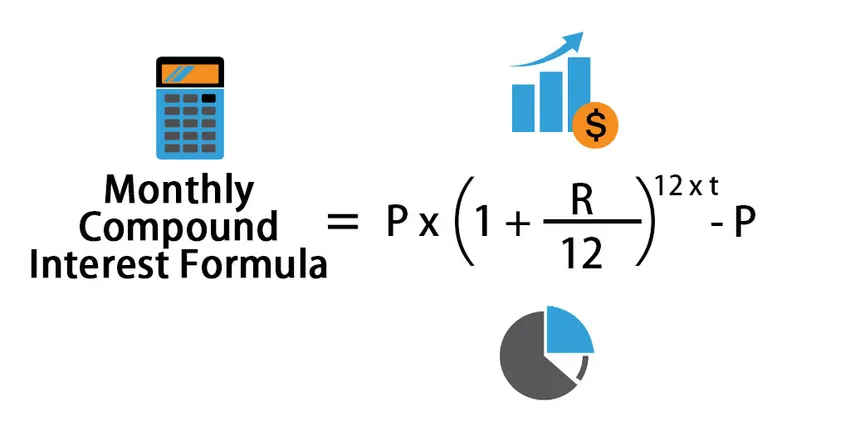
Formule d'intérêt composé mensuel - Exemples avec modèle Excel

Formule d'intérêt composé mensuel (Table des matières)

• Formule
• Exemples
• Calculatrice

Qu'est-ce que la formule d'intérêt composé mensuel?

Lorsqu'un certain montant d'argent est emprunté pour une durée spécifique, un montant supplémentaire doit être payé séparément avec le montant emprunté. Ensuite, le montant supplémentaire que nous payons au taux fixe est appelé intérêt. L'intérêt composé est l'intérêt total qui comprend l'intérêt d'origine et l'intérêt du nouveau principal qui est dégagé en ajoutant le principal d'origine à l'intérêt dû. Pour les mensualités composées à calculer, les intérêts qui sont composés tout le mois de l'année.

La formule d'intérêt composé mensuel peut être calculée comme suit:

Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P

où,

• P = montant du capital
• R = taux
• t = temps

Exemples de formule d'intérêt composé mensuel (avec modèle Excel)

Prenons un exemple pour mieux comprendre le calcul de l'intérêt composé mensuel.

Vous pouvez télécharger ce modèle Excel de formule d'intérêt mensuel composé ici - Modèle Excel de formule d'intérêt mensuel composé

Formule d'intérêt composé mensuel - Exemple # 1

Un emprunteur a emprunté une somme de 10 000 roupies au taux de 8%. Calculez le taux d'intérêt composé mensuel pour 2 ans?

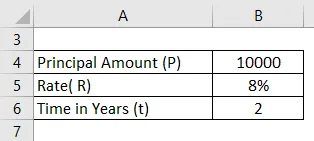
Solution:

L'intérêt composé mensuel est calculé à l'aide de la formule ci-dessous

Intérêt composé mensuel = P * (1 + (R / 12)) ^{12 * t} - P

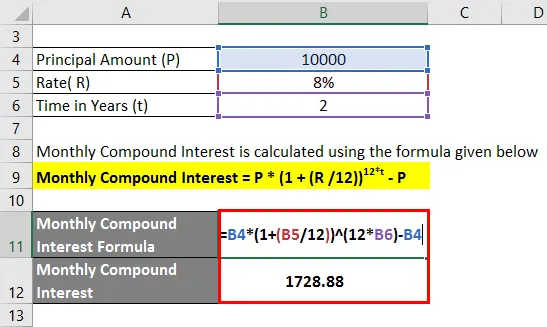
• Intérêt composé mensuel = 10 000 (1 + (8/12)) ^{2 * 12} - 10 000
• Intérêt composé mensuel = 1 728, 88

L'intérêt composé mensuel pour 2 ans est de Rs 1, 728.88

Formule d'intérêt composé mensuel - Exemple n ° 2

Une somme d'argent est investie au taux de 10% soit 20 000 roupies. Quels seront les intérêts composés mensuels pour les 10 ans?

Solution:

L'intérêt composé mensuel est calculé à l'aide de la formule ci-dessous

Intérêt composé mensuel = P * (1 + (R / 12)) ^{12 * t} - P

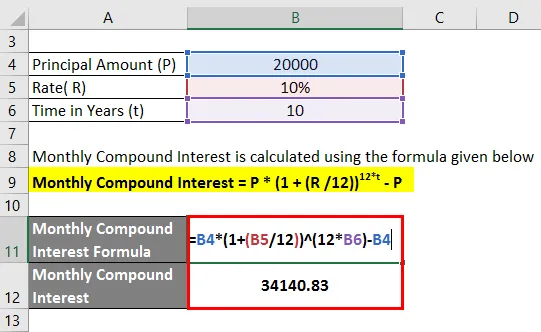
• Intérêt composé mensuel = 20 000 (1 + 10/12)) ^{10 * 12} - 20 000
• Intérêt composé mensuel = 34, 140.83

L'intérêt composé mensuel pour 10 ans est de Rs 34, 140.83

Formule d'intérêt composé mensuel - Exemple n ° 3

Mme Jefferson a acheté un statut d'antiquité pour 500 $. Cinq ans plus tard, elle a vendu ce statut pour 800 $. Elle le considérait comme faisant partie de l'investissement. Calculez le taux annuel qu'elle a obtenu?

Solution:

Si nous considérons un investissement de 500 $ et que nous obtenons 800 $ dans le futur, après t = 10 ans. Nous supposons un taux annuel m = 1 et l'implémentons dans la formule.

A = P (1 + r / m) ^mt

• 800 = 500 (1+ r / 1) ^{1 * 10}
• 800 = 500 (1 + r) ¹⁰

Maintenant, nous résolvons pour le taux (r) dans les étapes suivantes.

• 800 = 500 (1 + r) ¹⁰
• 8/5 = (1 + r) ¹⁰

Maintenant, nous prenons la puissance de (1/10) sur le côté gauche de l'équation et dégageons du côté droit.

• (8/5) ^1/10) = 1 + r

Calculez la valeur à gauche et résolvez pour r.

• 1, 0481 = 1 + r
• 1, 0481 - 1 = r
• 0, 0481 = r

Cependant, Mme Jefferson a gagné le taux d'intérêt annuel de 4, 81%, ce qui n'est pas un mauvais taux de rendement.

Explication

L'intérêt composé est le produit du montant du capital initial de un plus le taux d'intérêt annuel porté au nombre de périodes composées moins un. Ainsi, le montant initial du prêt est ensuite soustrait de la valeur résultante.

L'intérêt composé peut être calculé comme:

Formule d'intérêt composé = (P (1 + i) ⁿ ) - P

Formule d'intérêt composé = (P (1 + i) ⁿ - 1)

Où:

• P = montant du capital
• i = taux d'intérêt annuel en pourcentage
• n = périodes composées

Il existe un certain ensemble de procédures permettant de calculer les intérêts composés mensuels.

Étape 1: Nous devons calculer le montant des intérêts obtenus en utilisant les intérêts composés mensuels. La formule peut être calculée comme suit:

• A = (P (1 + i) ⁿ - 1) - P

Étape 2: si nous supposons que le taux d'intérêt est de 5% par an. Tout d'abord, nous devons exprimer la valeur du taux d'intérêt en nombre décimal équivalent. Cela peut être fait de la manière suivante.

• 5% = 5/100 = 0, 05

Étape 3: Comme nous savons que les intérêts sont composés mensuellement, nous pouvons donc prendre n = 12. Cependant, la période est spécifiée dans ce cas, nous considérons que le prêt est contracté pour une période d'un an. Maintenant, nous avons toutes les variables disponibles avec nous que nous pouvons directement remplacer dans la formule et en obtenir le résultat.

• A = 1000 ((1 + 0, 05 / 12) ¹² - 1)
• A = 1000 ((1 + 0, 0042) ¹² - 1)
• A = 1000 ((1, 0042) ¹² - 1)
• A = 1000 (1, 0516 - 1)
• A = 1000 (0, 0516)
• A = 51, 6

Nous avons calculé le taux d'intérêt pour 1 an par composition mensuelle à environ 51, 6

L'intérêt composé mensuel ne reflète pas les changements notables lorsque nous garons une certaine somme d'argent pour une durée à court terme. La raison en est qu'il faut plusieurs années pour que la composition donne des changements notables.

Et le plus important de l'intérêt composé est qu'il fait croître vos investissements plus rapidement que l'intérêt simple. Plus votre intervalle de composition est fréquent, plus la différence est importante ou nous pouvons dire que les intérêts composés quotidiens génèrent plus de revenus de vos investissements que les intérêts composés annuels pour un taux d'intérêt donné.

Le tableau suivant montre la différence que le nombre de périodes de composition peut faire sur une certaine période pour un prêt de 10 000 $ avec un taux d'intérêt annuel de 10% sur une période de 12 ans.

Fréquence de composition	Nombre de périodes de composition	Valeurs pour i et n	Intérêt total
Annuellement	1	I = 10%, n = 12	21 384, 2837 $
Semestriellement	2	I = 5%, n = 24	22 250 9994 $
Trimestriel	4	I = 2, 5%, n = 48	22 714, 8956 $
Mensuel	12	I = 0, 833%, n = 144	23 036, 4896 $

Pertinence et utilisations de la formule d'intérêt composé mensuel

L'intérêt composé s'est avéré le meilleur outil d'investissement, mais il peut être très dangereux s'il s'applique au montant de votre prêt. Vous finirez par payer plus d'intérêts sur le montant de votre prêt.

La composition devient plus efficace lorsque votre investissement est mensuel ou trimestriel plutôt qu'annuel, car il donne un meilleur rendement. Si vous empruntez de l'argent auprès d'une banque ou d'une institution financière, la composition annuelle est la meilleure option. Lorsque vous prêtez une certaine somme d'argent, la composition quotidienne sera plus productive. Mais nous devons garder à l'esprit que la composition peut être favorable ou défavorable selon les circonstances.

L'intérêt composé donne un meilleur retour sur votre investissement, dépend de la durée et de la taille de l'investissement. L'intérêt composé croît plus rapidement que vos attentes.

Les avantages de l'intérêt composé sont énumérés ci-dessous:

1. Réinvestissement
2. Meilleur retour sur investissement.
3. Économies à long terme.
4. Augmentation des revenus.

Calculateur de formule d'intérêt composé mensuel

Vous pouvez utiliser le calculateur de formule d'intérêt composé mensuel suivant

P
R
t
Formule d'intérêt composé mensuel

Formule d'intérêt composé mensuel =	P x ((1 + R / 12) 12 * t - P)
=	0 x ((1 +0/12) 12 * 0-0) = 0

Articles recommandés

Ceci est un guide de la formule d'intérêt composé mensuel. Ici, nous discutons de la façon de calculer la formule d'intérêt composé mensuel avec des exemples pratiques. Nous fournissons également un calculateur d'intérêt composé mensuel avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -

1. Formule pour le taux de croissance annuel composé
2. Comment calculer le taux d'intérêt nominal?
3. Formule d'intérêt composé quotidien
4. Guide de la formule de distribution de Poisson
5. Intérêt vs dividende | Les 8 principales différences que vous devez savoir