
Exemple de formule d'écart type (table des matières)
- Formule
- Exemples
Exemple de formule d'écart type
En statistique, l'écart type est essentiellement une mesure pour trouver la dispersion des valeurs de l'ensemble de données à partir de la valeur moyenne de l'ensemble de données. Il mesure la distance de ce point de données et la moyenne. Plus l'écart-type est élevé, plus la dispersion est grande et les points de données tendent à être loin de la moyenne. De même, un écart-type inférieur signifie que les points de données seront plus proches de la moyenne. Il est très utile pour comparer des ensembles de données qui peuvent avoir la même valeur moyenne mais une plage différente.
Habituellement, calculez l'écart-type des données démographiques, mais parfois les données démographiques sont si énormes qu'il n'est pas possible de trouver l'écart-type pour cela. Dans ce cas, l'écart type de l'échantillon est calculé et il deviendra le représentant de l'écart type de la population. Nous supposerons donc que l'échantillon est la représentation correcte de la population et nous nous concentrerons sur l'écart type de l'échantillon dans cet article.
Supposons que vous ayez un ensemble de données X avec des points de données (X1, X2 …… ..Xn).
La formule de l'écart-type de la population est donnée par:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Dans le cas où vous ne recevez pas la population entière et n'avez qu'un échantillon (disons que X est l'ensemble de données échantillon de la population), la formule de l'écart-type de l'échantillon est donnée par:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Où:
- X i - i ème valeur de l'ensemble de données
- X m - Valeur moyenne de l'ensemble de données
- n - Nombre total de points de données
La formule peut sembler déroutante au premier abord, mais c'est vraiment à travailler. Voici les étapes à suivre pour calculer l'écart type de l'échantillon:
- Trouver le nombre de points dans l'ensemble de données, c'est-à-dire n
- Ensuite, l'étape suivante consiste à trouver la valeur moyenne de l'échantillon. C'est fondamentalement la moyenne de toutes les valeurs.
- Après cela, pour chaque point de données, trouvez la différence entre celle-ci et la moyenne, puis ajustez-la.
- Prenez la somme de toutes les valeurs de l'étape ci-dessus et divisez-la par n-1.
- La dernière étape consiste à prendre la racine carrée du nombre calculé ci-dessus.
Il existe une autre façon de calculer la population et l'écart-type simplement en utilisant la fonction STDEV.P () pour l'écart-type de la population et la fonction STDEV.S () pour l'échantillon d'écart-type dans Excel.
Exemples d'échantillon de formule d'écart type (avec modèle Excel)
Prenons un exemple pour mieux comprendre le calcul de l'écart-type de l'échantillon.
Vous pouvez télécharger cet exemple de modèle Excel de formule d'écart type ici - Exemple de modèle Excel de formule d'écart typeExemple de formule d'écart type - Exemple # 1
Disons que nous avons deux exemples de jeux de données A et B et chacun contient 20 points de données aléatoires et ont la même moyenne. Calculez l'écart type de l'échantillon pour l'ensemble de données A et B.
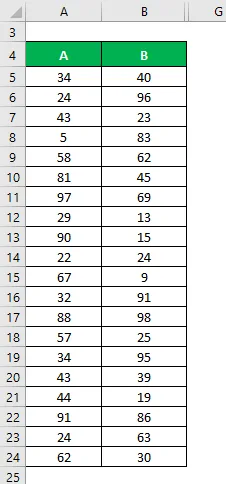
Solution:
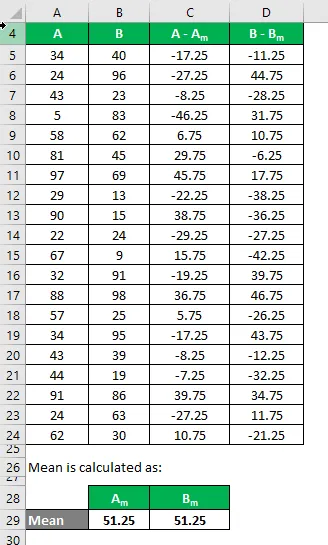
La moyenne est calculée comme suit:
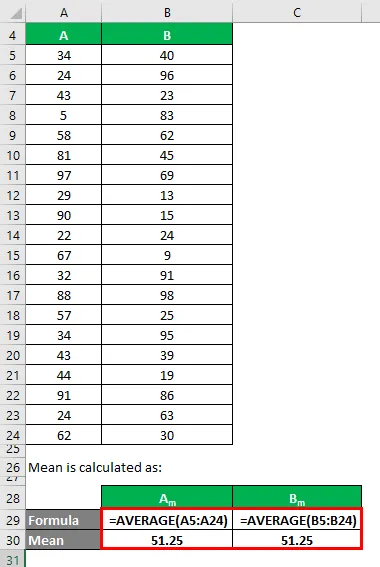
- Moyenne de l'ensemble de données A = 51, 25
- Moyenne de l'ensemble de données B = 51, 25
Maintenant, nous devons calculer la différence entre les points de données et la valeur moyenne.
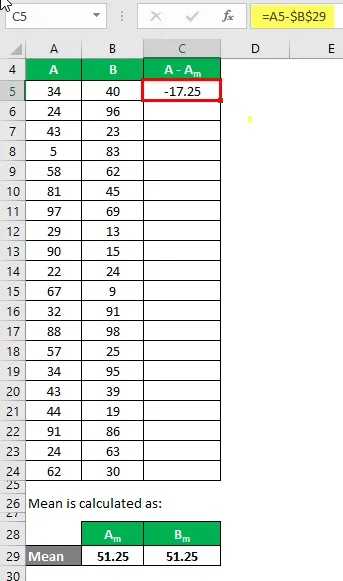
De même, calculez pour l'ensemble des données de A.
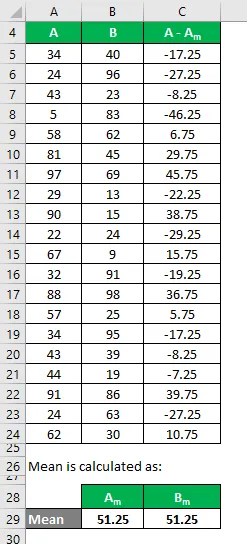
De même, calculez-le également pour l'ensemble de données B.
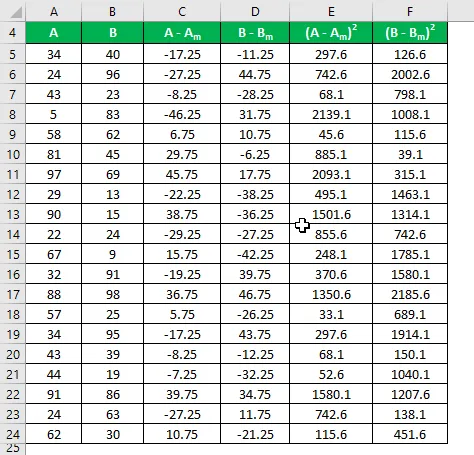
Calculez le carré de la différence pour les deux ensembles de données A et B.
L'écart type d'échantillon est calculé à l'aide de la formule ci-dessous
Écart type d'échantillon = √ (Σ (X i - X m ) 2 / (n - 1))
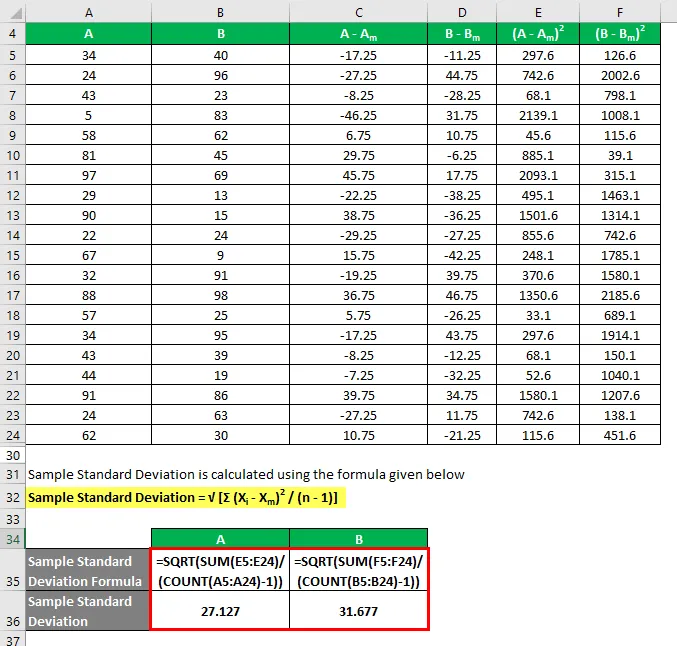
Donc, si vous voyez ici, bien que les deux ensembles de données aient la même valeur moyenne, B a un écart-type plus important que A, ce qui signifie que les points de données de B sont plus dispersés que A.
Exemple de formule d'écart type - Exemple # 2
Disons que vous êtes un investisseur très peu enclin au risque et que vous cherchez à investir de l'argent sur le marché boursier. Étant donné que votre appétit pour le risque est faible, vous souhaitez investir dans des actions sûres qui ont un écart-type plus faible. Votre conseiller financier vous a proposé 4 actions parmi lesquelles vous pouvez choisir. Vous souhaitez sélectionner 2 actions parmi ces 4 et vous le déciderez sur la base d'un écart type inférieur.
Vous avez des informations sur leurs rendements historiques des 15 dernières années.
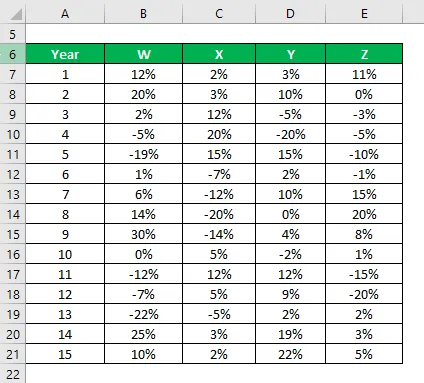
Solution:
L'échantillon d'écart type est calculé à l'aide de la formule Excel
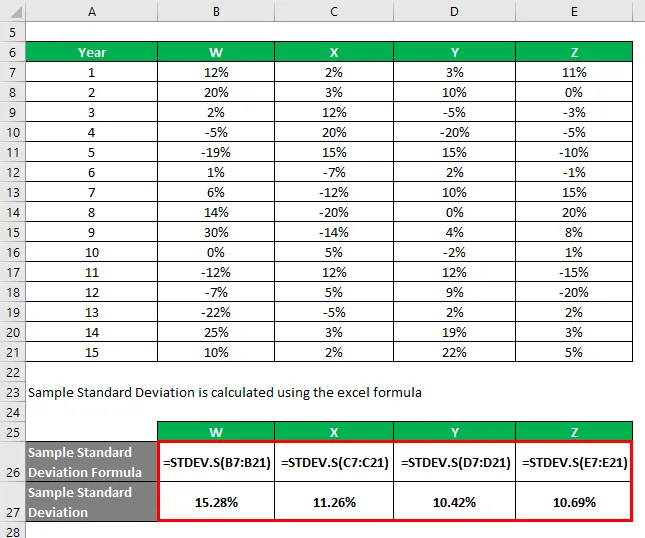
Sur la base des informations et de l'échantillon d'écart-type, vous choisirez les actions Y et Z à investir car elles ont l'écart-type le plus faible.
Explication
Nous discutons de la signification de l'écart-type d'un point de vue statistique, mais il joue également un rôle essentiel si nous parlons d'un point de vue financier. En finance, il s'agit essentiellement de la mesure du risque qu'un investissement comporte et de son degré de risque. En fonction du risque d'un investissement, les investisseurs peuvent ensuite calculer le rendement minimum dont ils ont besoin pour compenser ce risque. Comme dans l'exemple ci-dessus, puisque Y et Z ont un écart-type moindre, cela signifie qu'il y a moins de variabilité dans le rendement de ces actions, donc elles sont moins risquées. Un point lors de l'utilisation de l'outil d'écart-type, nous devons garder à l'esprit qu'il est fortement affecté par les valeurs extrêmes ou les valeurs aberrantes. Ces valeurs aberrantes peuvent fausser la valeur de l'écart-type.
Pertinence et utilisations de l'exemple de formule d'écart type
L'écart type aide les investisseurs et l'analyste à trouver le rapport risque / rendement ou ratio Sharpe pour un investissement. Fondamentalement, n'importe qui peut gagner un taux de rendement sans risque en investissant dans des titres du Trésor et sans risque. Mais le rendement en plus est le rendement excédentaire et pour y parvenir, quel est le niveau de risque que l'on doit prendre est une mesure du ratio de Sharpe:
Ratio de Sharpe = (retour sur investissement - taux sans risque) / écart type
Pour augmenter le ratio de Sharpe, l'investissement est meilleur.
Comme nous l'avons dit, l'écart-type est une mesure du risque, mais une valeur d'écart-type inférieure n'est pas toujours préférée. Si un investisseur a un appétit pour le risque plus élevé et souhaite investir de manière plus agressive, il sera disposé à prendre plus de risques et préférera un écart-type relativement plus élevé qu'un investisseur peu enclin à prendre des risques. Tout dépend donc du niveau de risque qu'un investisseur est prêt à prendre.
Articles recommandés
Ceci a été un guide pour l'exemple de formule d'écart type. Ici, nous discutons comment calculer l'écart type d'échantillon avec des exemples pratiques et un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Exemples de formule de variance de la population
- Calculatrice pour l'écart type relatif
- Comment calculer la distribution normale standard?
- Calcul de la distribution binomiale