Exemple d'intérêt composé - Exemples pratiques avec formule | Développement de l'entrepreneuriat 2025

Introduction à l'exemple d'intérêt composé

Il existe de nombreux exemples d'intérêts composés. L'exemple différent d'intérêt composé suivant donne une compréhension du type le plus courant de situations où l'intérêt composé est calculé et comment on peut le calculer. Comme il existe plusieurs domaines et situations dans lesquels l'intérêt composé peut être calculé, il n'est pas possible de fournir tous les types d'exemples. Ainsi, certains des exemples d'intérêt composé sont donnés ci-dessous montrant les différentes situations

Exemples d'intérêts composés (avec modèle Excel)

Prenons un exemple pour mieux comprendre le calcul de l'intérêt composé.

Vous pouvez télécharger cet exemple de modèle Excel d'intérêt composé ici - Exemple de modèle Excel d'intérêt composé Voici les exemples de l'intérêt composé:

Exemple d'intérêt composé -1

Harry veut commencer à économiser sur l'argent gagné par lui. Il décide alors de déposer le montant initial de 10 000 $ dans le compte d'épargne à intérêt élevé. Le taux d'intérêt, dans ce cas, sera de 15% par an composé annuellement. Actuellement, l'âge de harry est de 40 ans et il prévoit de prendre sa retraite à l'âge de 60 ans. Cela signifie que Harry a un horizon de 40 ans sur lequel il peut accumuler l'intérêt. Calculez le montant d'argent que Harry va recevoir à l'âge de 60 ans. Préparez également le tableau pour montrer l'intérêt annuel et la valeur du compte.

Donné,

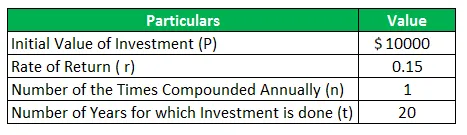
Solution:

À l'aide des informations fournies, le calcul de l'intérêt composé et du montant à recevoir à l'âge de 60 ans est le suivant:

Le calcul de la valeur future de l'investissement à l'aide de la formule d'intérêt composé est le suivant:

A = P (1 + r / n) ^nt

A = 10 000 $ (1 + 0, 15 / 1) ^{1 * 20}
A = 10 000 $ (1 + 0, 15) ²⁰
A = 10 000 $ (1, 15) ²⁰
A = 10 000 $ * 16, 367
A = 163 665, 37 $

Tableau pour montrer l'intérêt annuel et la valeur du compte

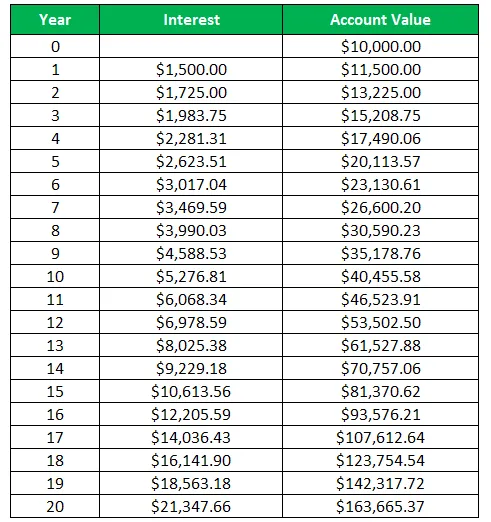
Ici, l'intérêt est calculé comme suit:

Intérêt = Montant initial de l'investissement * Taux d'intérêt (r)
Intérêt = 10000 * 15%
Intérêt = 1500 $

De même pour toutes les années.

et la valeur du compte est calculée comme suit:

Valeur du compte = montant initial de l'investissement + intérêts
Valeur du compte = 10000 + 1500
Valeur du compte = 11500 $

De même pour toutes les années.

Dans le présent exemple, nous pouvons voir que la valeur au compte de l'investissement effectué initialement de 10 000 $ devient 163 665, 37 $ à la fin de la période de 20 ans. Cela met en évidence la puissance de la composition, car avec l'aide des intérêts composés, Harry a multiplié son argent en plusieurs fois sans gérer activement l'investissement. Ici, le Harry a pu également gagner des intérêts sur les intérêts précédemment gagnés.

Exemple d'intérêt composé -2

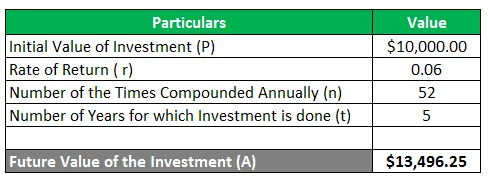
Sam fait un investissement initial de 10 000 $ pour une période de 5 ans. Il veut connaître le montant de l'investissement qu'il obtiendra après les 5 ans si l'investissement gagne le rendement de 6% par an composé hebdomadairement.

Donné,

En utilisant les informations fournies, le calcul de l'intérêt composé et du montant à recevoir après la période de 5 ans est le suivant:

Solution:

Le calcul de la valeur future d'un investissement à l'aide de la formule d'intérêt composé est le suivant:

A = P (1 + r / n) ^nt

A = 10 000 $ (1 + 0, 6 / 52) ^{52 * 5}

A = 10 000 $ (1 + 0, 00115) ²⁶⁰

A = 10 000 $ (1, 00115) ²⁶⁰

A = 10 000 $ * 1, 3496

A = 13 496, 25 $

Dans le présent exemple, nous pouvons voir que la valeur au compte de l'investissement effectué initialement de 10 000 $ devient 13 496, 25 $ à la fin de la période de 5 ans lorsque la composition est effectuée sur une base hebdomadaire. La composition augmente la valeur de l'investissement à la fin de la période, car les intérêts sont également gagnés sur les intérêts précédemment gagnés. Ici, le compoundage est effectué 52 fois car il y a 52 semaines dans une année.

Conclusion - Exemple d'intérêt composé

L'intérêt composé donne plus d'intérêt par rapport à l'intérêt simple car il est dérivé en facturant des intérêts sur le principal impayé, y compris les intérêts contrairement aux intérêts simples où des intérêts sont facturés sur le montant principal initial et aucun intérêt sur les intérêts n'est facturé. La puissance de la composition aide à accroître l'investissement avec plus de rapidité grâce aux caractéristiques de la fonction exponentielle. C'est le résultat du fait qu'en dépit de l'investissement, ils sont réinvestis pour croître plus rapidement. Ceci est très souvent utilisé dans les pratiques commerciales normales, que ce soit le prêt ou le dépôt. De plus, la fréquence à laquelle la composition est effectuée sera également un facteur déterminant pour la croissance. Supposons que, à un taux donné, la fréquence de composition soit par mois, alors son taux annualisé sera supérieur à celui de la fréquence de composition semestriellement ou annuellement.

Articles recommandés

Ceci a été un guide pour l'exemple d'intérêt composé. Nous discutons ici comment calculer l'intérêt composé à l'aide de sa formule ainsi que des exemples pratiques. Vous pouvez également consulter les articles suivants pour en savoir plus -