Introduction à l'algorithme de clustering hiérarchique
L'algorithme de clustering hiérarchique est une technique d'apprentissage automatique non supervisée. Il vise à trouver un regroupement naturel en fonction des caractéristiques des données.
L'algorithme de clustering hiérarchique vise à trouver des groupes imbriqués de données en construisant la hiérarchie. Elle est similaire à la taxonomie biologique du règne végétal ou animal. Les grappes hiérarchiques sont généralement représentées à l'aide de l'arborescence hiérarchique connue sous le nom de dendrogramme.
Types d'algorithme de clustering hiérarchique
Les algorithmes de clustering hiérarchiques sont de 2 types:
- Diviseur
- Agglomératif
1. Diviseur
Il s'agit d'une approche descendante, où elle considère initialement l'ensemble des données comme un seul groupe, puis divise de manière itérative les données en sous-groupes. Si le nombre d'un algorithme de clustering hiérarchique est connu, le processus de division s'arrête une fois le nombre de clusters atteint. Sinon, le processus s'arrête lorsque les données ne peuvent plus être divisées, ce qui signifie que le sous-groupe obtenu à partir de l'itération actuelle est le même que celui obtenu à partir de l'itération précédente (on peut également considérer que la division s'arrête lorsque chaque point de données est un cluster ).
2. Agglomération
Il s'agit d'une approche ascendante qui repose sur la fusion de clusters. Initialement, les données sont divisées en m grappes singleton (où la valeur de m est le nombre d'échantillons / points de données). Deux clusters sont fusionnés en un seul de manière itérative, ce qui réduit le nombre de clusters à chaque itération. Ce processus de fusion de clusters s'arrête lorsque tous les clusters ont été fusionnés en un seul ou que le nombre de clusters souhaité est atteint.
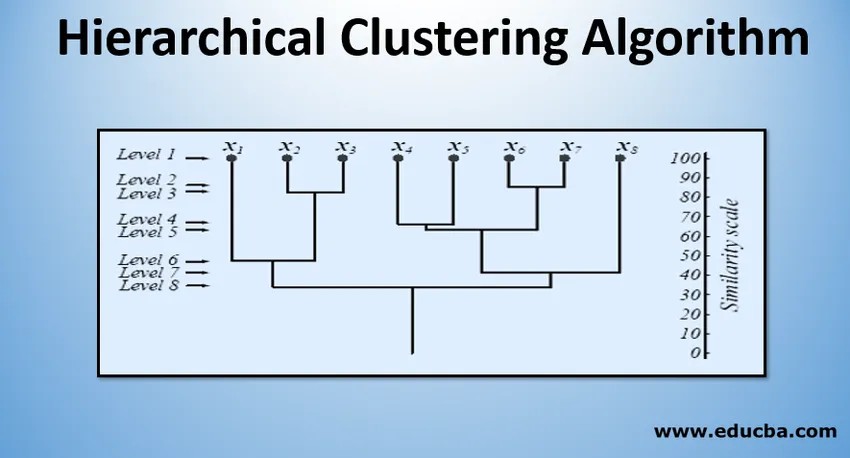
Au niveau 1, il y a m clusters qui sont réduits à 1 cluster au niveau m. Les points de données qui sont fusionnés pour former un cluster à un niveau inférieur restent également dans le même cluster aux niveaux supérieurs. Par exemple, supposons qu'il y ait 8 points x1..x8, donc initialement, il y a 8 clusters au niveau 1. Supposons que les points x1 et x2 soient fusionnés en un cluster au niveau 2, puis jusqu'au niveau 8, ils restent dans le même cluster.
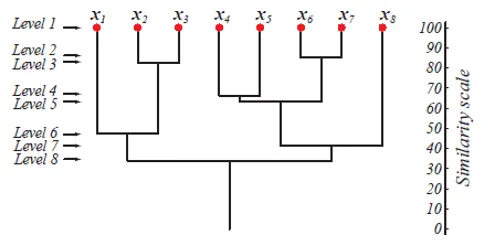
La figure ci-dessus montre une représentation par dendrogramme de l'approche de regroupement d'agglomération pour 8 points de données ainsi que l'échelle de similitude correspondant à chaque niveau.
Les niveaux de grappes nous donnent une idée de la similitude des points de données dans les grappes. Comme le montre la figure 1, plus tôt les points de données sont fusionnés dans un cluster, les mêmes qu'ils sont. Ainsi, les points de données d'un cluster de niveau 2 (par exemple, x2 et x3) sont plus similaires que ces points de données d'un cluster de niveau 6 (par exemple, x1 et x2).
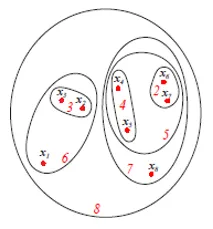
La figure ci-dessus montre la représentation du diagramme de Set ou de Venn de l'approche d'agrégation agglomérative des 8 points de données mentionnés ci-dessus. Les dendrogrammes et les représentations d'ensemble peuvent être utilisés pour le regroupement. Cependant, un dendrogramme est généralement préférable. La représentation des actifs ne peut pas représenter quantitativement les similitudes des clusters.
Étapes pour l'algorithme de clustering hiérarchique
Suivons les étapes suivantes pour l'algorithme de clustering hiérarchique qui sont données ci-dessous:
1. Algorithme
Algorithme d'agrégation hiérarchique agglomératif
- Commencez à initialiser c, c1 = n, Di = (xi), i = 1, …, n '
- Do c1 = c1 - 1
- Trouvez les clusters les plus proches, disons Di et Dj
- Fusionner Di et Dj
- Jusqu'à c = c1
- Retourner les clusters C
- Fin
Cet algorithme commence par n clusters initialement où chaque point de données est un cluster. À chaque itération, le nombre de clusters diminue de 1 lorsque les 2 clusters les plus proches sont fusionnés. Ce processus se poursuit jusqu'à ce que le nombre de clusters se réduise à la valeur prédéfinie c.
Comment décider quels clusters sont proches?
Cela est défini à l'aide de plusieurs mesures de distance qui sont les suivantes:
- La distance minimale entre les clusters dmin (Di, Dj). Utile pour célibataire.
- La distance maximale entre les clusters dmax (Di, Dj). Utile pour complet.
- La distance moyenne entre les clusters davg (Di, Dj).
Qu'est-ce que la liaison simple et la liaison complète?
- Lorsque dmin (di, dj) est utilisé pour trouver la distance entre deux clusters, et que l'algorithme se termine si la distance entre les clusters les plus proches dépasse un seuil, l'algorithme est alors appelé un algorithme de liaison unique.
- Lorsque dmax (Di, Dj) est utilisé pour trouver la distance entre deux clusters et que l'algorithme se termine si la distance entre les clusters les plus proches dépasse un seuil, l'algorithme est alors appelé algorithme de liaison complet.
- Considérons chaque point de données comme un nœud d'un graphe. Il y a un bord entre deux points de données s'ils appartiennent au même cluster. Lorsque deux clusters les plus proches sont fusionnés, une arête est ajoutée. C'est ce qu'on appelle une liaison unique car il existe un chemin unique d'un nœud à l'autre.
- L'algorithme de liaison complet fusionne deux clusters en minimisant la distance entre les deux points les plus éloignés.
- Un algorithme de liaison unique génère un arbre couvrant. Cependant, cet algorithme est sensible au bruit. Un algorithme de liaison complet génère un graphique complet.
Quelle est la complexité temporelle de l'algorithme?
Supposons que nous ayons n motifs dans l'espace d-dimensionnel, et que nous utilisons dmin (Di, Dj) pour former c grappes. Nous devons calculer n (n - 1) distances inter-points - dont chacun est un calcul O (d 2 ) - et placer les résultats dans un tableau de distance inter-points. La complexité spatiale est O (n 2 ). Pour trouver la paire de distances minimales (pour la première fusion), nous devons parcourir la liste complète, en gardant l'indice de la plus petite distance.
Ainsi pour la première étape agglomérative, la complexité est O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Pour une autre étape d'agglomération arbitraire (c.-à-d. De c1 à c1 - 1), nous parcourons simplement les n (n - 1) - c1 distances «inutilisées» dans la liste et trouvons la plus petite pour laquelle x et x 'se trouvent dans des grappes différentes . C'est, encore une fois, O (n (n − 1) −c1). La complexité temporelle totale est donc O (cn 2 d 2 ), et dans des conditions typiques n >> c.
2. Visualisation
Une fois les données divisées en grappes, il est recommandé de visualiser les grappes afin d'avoir une idée de l'apparence du regroupement. Mais visualiser ces données de grande dimension est difficile. Par conséquent, nous utilisons l'analyse en composantes principales (ACP) pour la visualisation. Après l'ACP, nous obtenons les points de données dans l'espace de faible dimension (généralement 2D ou 3D) que nous pouvons tracer pour voir le regroupement.
Remarque: Une dimension élevée signifie un grand nombre de fonctionnalités et non un certain nombre de points de données.3. Évaluation
L'une des méthodes d'évaluation des grappes est que la distance des points entre les grappes (distance inter-grappes) doit être bien supérieure à la distance des points à l'intérieur du grappe (distance intracluster).
Conclusion
Voici les quelques points clés à retenir:
- L'algorithme de clustering hiérarchique est utilisé pour trouver des modèles imbriqués dans les données
- Le clustering hiérarchique est de 2 types - Diviseur et Agglomératif
- Le dendrogramme et le diagramme set / Venn peuvent être utilisés pour la représentation
- La liaison simple fusionne deux clusters en minimisant la distance minimale entre eux. Il forme une étendue
- La liaison complète fusionne deux clusters en minimisant la distance maximale entre Elle forme un graphique complet.
- La complexité temporelle totale de l'algorithme de clustering hiérarchique est O (cn 2 d 2 ), où c est le nombre prédéfini de clusters, n est le nombre de motifs et d est l'espace en d dimensions des n motifs.
Articles recommandés
Ceci est un guide de l'algorithme de clustering hiérarchique. Nous discutons ici des types et des étapes des algorithmes de clustering hiérarchiques. Vous pouvez également consulter les articles suivants pour en savoir plus-
- Analyse de regroupement hiérarchique
- Regroupement hiérarchique dans R '
- Algorithme de clustering
- Qu'est-ce que le clustering dans l'exploration de données?
- Regroupement hiérarchique | Clustering Agglomératif & Diviseur
- Algorithme C ++ | Exemples d'algorithme C ++