Introduction au clustering hiérarchique
- Récemment, un de nos clients a demandé à notre équipe de publier une liste de segments avec un ordre d'importance au sein de leurs clients pour les cibler à franchiser l'un de leurs produits nouvellement lancés. Clairement, la simple segmentation des clients à l'aide du clustering partiel (k-means, c-fuzzy) ne fera pas ressortir l'ordre d'importance où le clustering hiérarchique entre en jeu.
- Le clustering hiérarchique sépare les données en différents groupes sur la base de certaines mesures de similitude appelées clusters, qui visent essentiellement à créer la hiérarchie entre les clusters. Il s'agit essentiellement d'un apprentissage non supervisé et le choix des attributs pour mesurer la similitude est spécifique à l'application.
Le cluster de la hiérarchie des données
- Clustering agglomératif
- Clustering diviseur
Prenons un exemple de données, notes obtenues par 5 étudiants pour les regrouper lors d'un prochain concours.
| Étudiant | Des marques |
| UNE | dix |
| B | sept |
| C | 28 |
| ré | 20 |
| E | 35s |
1. Clustering agglomératif
- Pour commencer, nous considérons chaque point / élément individuel ici comme des grappes et continuons à fusionner les points / éléments similaires pour former un nouveau cluster au nouveau niveau jusqu'à ce que nous nous retrouvions avec le cluster unique est une approche ascendante.
- La liaison unique et la liaison complète sont deux exemples populaires de regroupement agglomératif. Autre que cette liaison moyenne et liaison Centroid. En liaison simple, nous fusionnons à chaque étape les deux clusters, dont les deux membres les plus proches ont la plus petite distance. En liaison complète, nous fusionnons dans les membres de la plus petite distance qui fournissent la plus petite distance maximale par paire.
- Matrice de proximité, c'est le noyau pour effectuer un clustering hiérarchique, qui donne la distance entre chacun des points.
- Faisons une matrice de proximité pour nos données données dans le tableau, puisque nous calculons la distance entre chacun des points avec d'autres points ce sera une matrice asymétrique de forme n × n, dans notre cas 5 × 5 matrices.
Une méthode populaire pour les calculs de distance est:
- Distance euclidienne (au carré)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Distance de Manhattan
dist((x, y), (a, b)) =|x−c|+|y−d|
La distance euclidienne est la plus couramment utilisée, nous utiliserons la même chose ici, et nous utiliserons une liaison complexe.
| Étudiant (grappes) | UNE | B | C | ré | E |
| UNE | 0 | 3 | 18 | dix | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | sept |
| ré | dix | 13 | 8 | 0 | 15 |
| E | 25 | 28 | sept | 15 | 0 |
Les éléments diagonaux de la matrice de proximité seront toujours 0, car la distance entre le point avec le même point sera toujours 0, donc les éléments diagonaux sont exemptés de considération pour le regroupement.
Ici, dans l'itération 1, la plus petite distance est 3, donc nous fusionnons A et B pour former un cluster, formons à nouveau une nouvelle matrice de proximité avec le cluster (A, B) en prenant (A, B) le point de cluster comme 10, c'est-à-dire maximum de ( 7, 10) donc la matrice de proximité nouvellement formée serait
| Clusters | (UN B) | C | ré | E |
| (UN B) | 0 | 18 | dix | 25 |
| C | 18 | 0 | 8 | sept |
| ré | dix | 8 | 0 | 15 |
| E | 25 | sept | 15 | 0 |
Dans l'itération 2, 7 est la distance minimale, donc nous fusionnons C et E pour former un nouveau cluster (C, E), nous répétons le processus suivi dans l'itération 1 jusqu'à ce que nous nous retrouvions avec le cluster unique, ici nous nous arrêtons à l'itération 4.
L'ensemble du processus est illustré dans la figure ci-dessous:
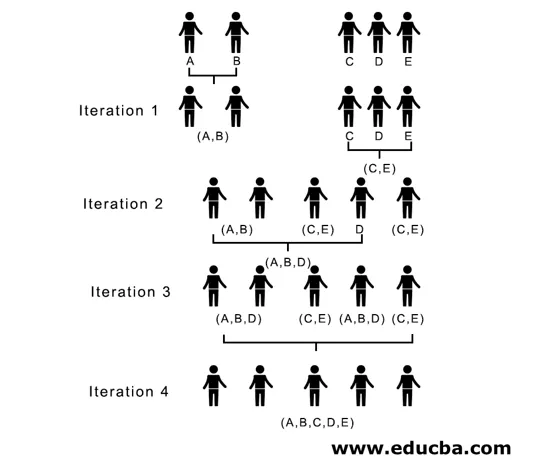
(A, B, D) et (D, E) sont les 2 grappes formées à l'itération 3, à la dernière itération, nous pouvons voir que nous nous retrouvons avec une seule grappe.
2. Clustering diviseur
Pour commencer, nous considérons tous les points comme un seul cluster et les séparons par la distance la plus éloignée jusqu'à ce que nous terminions avec des points individuels comme des clusters individuels (pas nécessairement nous pouvons nous arrêter au milieu, cela dépend du nombre minimum d'éléments que nous voulons dans chaque cluster) à chaque étape. C'est tout le contraire du clustering aggloméré et c'est une approche descendante. Le regroupement par division est une façon dont k répétitif signifie regroupement.
Le choix entre l'agglomération et le clustering diviseur dépend à nouveau de l'application, mais peu de points à considérer sont:
- La division est plus complexe que le regroupement aggloméré.
- Le clustering diviseur est plus efficace si nous ne générons pas une hiérarchie complète jusqu'aux points de données individuels.
- Le clustering agglomératif prend une décision en considérant les patters locaux, sans tenir compte au départ de schémas globaux qui ne peuvent être inversés.
Visualisation du clustering hiérarchique
Une méthode super utile pour visualiser le clustering hiérarchique qui aide dans les affaires est le dendogramme. Les dendogrammes sont des structures arborescentes qui enregistrent la séquence de fusion et de fractionnement dans laquelle la ligne verticale représente la distance entre les grappes, la distance entre les lignes verticales et la distance entre les grappes est directement proportionnelle, c'est-à-dire plus la distance plus les grappes sont susceptibles d'être différentes.
Nous pouvons utiliser le dendogramme pour décider du nombre de grappes, il suffit de tracer une ligne qui coupe avec une ligne verticale la plus longue sur le dendogramme, un certain nombre de lignes verticales intersectées sera le nombre de grappes à considérer.
Voici l'exemple de Dendogramme.
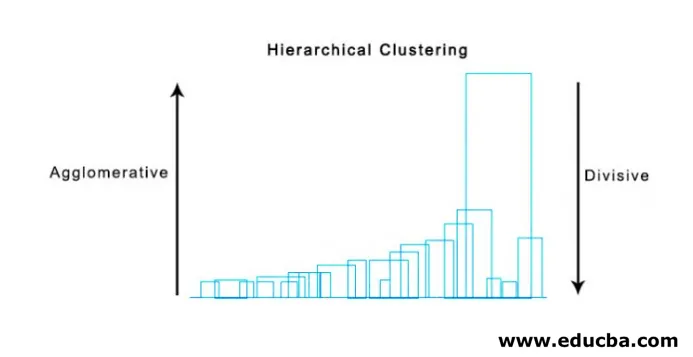
Il existe des packages python assez simples et directs et ses fonctions permettent d'effectuer un clustering hiérarchique et de tracer des dendogrammes.
- La hiérarchie de scipy.
- Cluster.hierarchy.dendogram pour la visualisation.
Scénarios courants dans lesquels le clustering hiérarchique est utilisé
- Segmentation de la clientèle vers le marketing de produits ou de services.
- Planification de la ville pour identifier les endroits pour construire des structures / services / bâtiment.
- Analyse des réseaux sociaux, par exemple, identifiez tous les fans de MS Dhoni pour annoncer son biopic.
Avantages du clustering hiérarchique
Les avantages sont donnés ci-dessous:
- Dans le cas d'un clustering partiel comme k-means, le nombre de clusters doit être connu avant le clustering, ce qui n'est pas possible dans les applications pratiques, tandis que dans le clustering hiérarchique aucune connaissance préalable du nombre de clusters n'est requise.
- Le clustering hiérarchique génère une hiérarchie, c'est-à-dire une structure plus informative que l'ensemble non structuré des clusters plats renvoyés par le clustering partiel.
- Le clustering hiérarchique est facile à implémenter.
- Fait ressortir des résultats dans la plupart des scénarios.
Conclusion
Le type de clustering fait la grande différence lorsque les données sont présentées, le clustering hiérarchique étant plus informatif et plus facile à analyser est préférable au clustering partiel. Et il est souvent associé à des cartes de chaleur. Sans oublier les attributs choisis pour calculer la similitude ou la dissimilarité qui influencent principalement les clusters et la hiérarchie.
Articles recommandés
Ceci est un guide du clustering hiérarchique. Nous discutons ici de l'introduction, des avantages du clustering hiérarchique et des scénarios courants dans lesquels le clustering hiérarchique est utilisé. Vous pouvez également consulter nos autres articles suggérés pour en savoir plus–
- Algorithme de clustering
- Clustering dans l'apprentissage automatique
- Regroupement hiérarchique dans R
- Méthodes de regroupement
- Comment supprimer la hiérarchie dans Tableau?