Formule CAPM (Table des matières)
- Formule CAPM
- CAPM Calculator
- Formule CAPM dans Excel (avec modèle Excel)
Formule CAPM
La relation linéaire entre le retour sur investissement attendu et son risque systématique est représentée par la formule du modèle CAPM (Capital Asset Pricing Model).
Le CAPM est calculé selon la formule ci-dessous: -
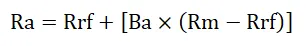
Où:
- Ra = Retour attendu sur investissement
- Rrf = taux sans risque
- Ba = bêta de l'investissement
- Rm = Rendement attendu sur le marché
Et la prime de risque est la différence entre le rendement attendu du marché moins le taux sans risque (Rm - Rrf) .
Prime de risque de marché
La prime de risque de marché est le rendement excédentaire, c'est-à-dire la récompense censée compenser un investisseur pour la prise du risque inhérent au portefeuille, car investir dans le marché boursier est toujours plus élevé que d'investir dans des obligations d'État. Il s'agit donc d'une différence entre le rendement attendu du marché et le taux sans risque. Le taux de rendement du marché, Rm, peut être estimé en fonction des rendements passés ou des rendements futurs projetés. Par exemple, les bons du Trésor et les obligations des États-Unis sont utilisés pour le taux sans risque.
Retour attendu
Le «Ra» fait référence au rendement attendu d'un investissement sur la période de temps.
Taux sans risque
Le «Rrf» désigne le taux sans risque, qui est égal au rendement d'un bon du Trésor américain à 10 ans ou d'une obligation gouvernementale. Le taux sans risque est le rendement d'un investissement qui ne génère aucun risque, mais dans le monde réel, il inclut le risque d'inflation. Le taux sans risque devrait également être celui du pays où l'investissement est effectué et la période d'échéance de l'obligation devrait également correspondre à la période de l'investissement. Normalement, le taux de rendement sans risque qui est utilisé pour estimer la prime de risque est généralement la moyenne des taux de rendement sans risque historiques et non généralement le taux de rendement sans risque actuel.
Bêta
Le bêta qui est représenté comme «Ba» dans les formules de CAPM est une mesure de la volatilité d'un titre ou d'un portefeuille et est calculé en mesurant dans quelle mesure le cours de l'action change avec le retour du marché global. La bêta est une mesure du risque systématique. Par exemple, si le bêta d'une entreprise est égal à 1, 7, cela signifie qu'elle a 170% de la volatilité des rendements de la moyenne du marché et que les mouvements des cours des actions seront plutôt extrêmes. Si le bêta est égal à 1, le retour sur investissement attendu est égal au rendement de la moyenne du marché. Si le bêta est -1, cela signifie que les cours des actions sont moins risqués et volatils.
Application du modèle CAPM
Nous verrons quelques exemples de CAPM qui sont le plus souvent utilisés pour déterminer quel devrait être le juste prix d'un investissement. Lorsque nous calculons le taux de rendement de l'actif risqué à l'aide de CAPM, ce taux peut également être utilisé pour actualiser les flux de trésorerie futurs de l'investissement à leur valeur actuelle et finalement arriver au juste prix de l'investissement.
Exemples de formule CAPM
Prenons un exemple pour découvrir le CAPM d'une entreprise: -
Vous pouvez télécharger ce modèle Excel de formule CAPM ici - Modèle Excel de formule CAPMExemple 1
Supposons que l'action A devrait générer des rendements de 14% au cours de la prochaine année et que le taux sans risque actuel soit de 6%, et vous souhaitez calculer s'il est rentable d'investir dans ce domaine. Vous avez calculé la valeur bêta de l'action qui est de 1, 7. Le marché boursier global a un bêta de 1, 0. Cela implique que l'action comporte un niveau de risque plus élevé que le risque global. Par conséquent, nous prévoyons un rendement supérieur au rendement prévu du marché de 14% au cours de la prochaine année.
Le retour attendu peut être calculé comme suit:
- Retour requis (Ra) = Rrf + (Ba * (Rm - Rrf))
- Rendement requis (Ra) = 6% + 1, 7 * (14% - 6%)
- Rendement requis (Ra) = 6% + 13, 6%
- Rendement requis (Ra) = 19, 6%
Ce calcul vous indique que vous obtiendrez 19, 6% sur votre investissement.ca
Exemple 2
Supposons qu'un investisseur envisage d'investir dans l'une des trois actions disponibles sur le marché. Les informations ci-dessous sont disponibles pour estimer le taux de rendement des trois stocks.
- Stock A avec un bêta de 0, 80
- Stock B avec un bêta de 1, 20
- Stock C avec un bêta de 1, 50
Le taux sans risque est de 5, 00% et le rendement du marché attendu est de 12, 00%.
Nous pouvons calculer le rendement attendu de chaque stock avec la formule CAPM.
- Retour requis (Ra) = Rrf + (Ba * (Rm - Rrf))
Retour prévu du stock A
- E (R A ) = 5, 0% + 0, 80 * (12, 00% - 5, 0%)
- E (R A ) = 5, 0% + 5, 6%
- E (R A ) = 10, 6%
Retour prévu du stock B
- E (R B ) = 5, 0% + 1, 20 * (12, 00% - 5, 0%)
- E (R B ) = 5, 0% + 8, 4%
- E (R B ) = 13, 4%
Retour prévu du stock C
- E (R C ) = 5, 0% + 1, 50 * (12, 00% - 5, 0%)
- E (R C ) = 5, 0% + 10, 5%
- E (R C ) = 15, 5%
Par conséquent, nous voyons qu'il est préférable d'investir dans l'action C. Donc, on voit que plus le bêta est élevé, plus le rendement attendu selon la formule CAPM sera élevé.
Exemple 3
Nous allons maintenant voir un problème d'application de retour attendu. Nous pouvons calculer la valeur actuelle nette en utilisant le rendement attendu ou le taux d'obstacle de la formule CAPM comme taux actualisé pour estimer la valeur actuelle nette d'un investissement
Les informations suivantes sont données:
- β = 1, 3
- Rrf = 6%
- Rm = 13%
Ainsi, le taux d'obstacle ou le rendement attendu du projet est calculé comme suit:
- Retour requis (Ra) = Rrf + (Ba * (Rm - Rrf))
- Ra = 6% + 1, 3 * (13% - 6%)
- Ra = 6% + 9, 1%
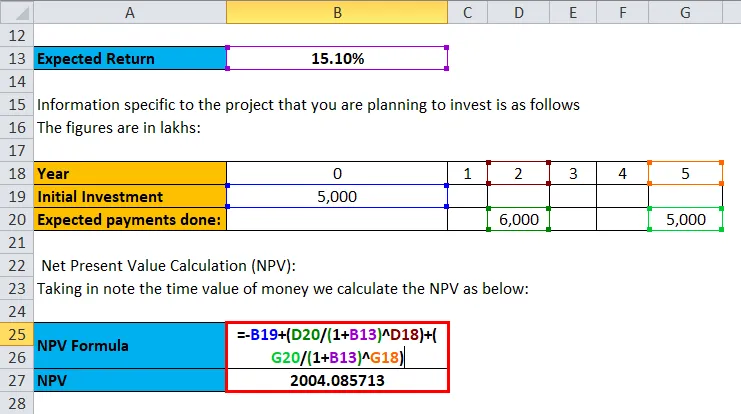
- Ra = 15, 1%
Les informations spécifiques au projet que vous envisagez d'investir sont les suivantes. Les chiffres sont en lakhs:
- Investissement initial = 5 000 ₹
- Paiements attendus: 6 000 ₹ en 2 e année, 5 000 ₹ en 5 e année
Calcul de la valeur actuelle nette (VAN): En prenant en note la valeur temps de l'argent, nous calculons la VAN comme suit:
Npv = - investissement initial + somme de (valeur de l'investissement / (taux 1+) nombre d'années)
L'investissement initial est donc de 5 000, puis 6 000 sont investis la deuxième année et 5 000 la 5 e année. il suffit de mettre les valeurs pour obtenir les résultats
- VAN = -5 000 + (6 000 / 1, 151 2) + (5 000 / 1, 151 5)
- NPV = ₹ 2004.085713
Par conséquent, la valeur nette de l'investissement effectué est de ₹ 2004.085713.
Hypothèses de la formule CAPM
- Les investisseurs détiennent une diversification sur une gamme d'investissements afin d'éliminer les risques non systématiques.
- Les investisseurs peuvent prêter et emprunter tout montant sous le taux sans risque.
- CAPM considère qu'un marché est idéal et n'inclut pas la fiscalité ni aucun coût de transaction dans un compte.
- Supposons que toutes les informations soient disponibles en même temps pour tous les investisseurs.
- Chaque investisseur est contre l'exposition au risque.
Limites
La limitation de cette formule CAPM est d'autant plus élevée que le risque de l'actif est élevé, plus le rendement attendu est élevé, ce qui n'est pas toujours vrai.
Calculateur de formule CAPM
Vous pouvez utiliser le calculateur CAPM suivant
| Rrf (%) | |
| Ba | |
| Rm (%) | |
| Ra | |
| Ra = Rrf + (Ba X (Rm - Rrf)) |
| 0 + (0 X (0-0)) = 0 |
Formule CAPM dans Excel (avec modèle Excel)
Ici, nous ferons le même exemple de la formule CAPM dans Excel. C'est très facile et simple. Vous devez fournir les trois entrées, à savoir le taux sans risque, le bêta de l'investissement et le retour attendu sur le marché
Vous pouvez facilement calculer le CAPM en utilisant la formule dans le modèle fourni.
Le retour attendu peut être calculé comme suit:
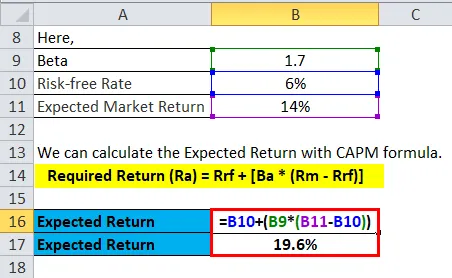
Nous pouvons calculer le rendement attendu de chaque stock avec la formule CAPM.
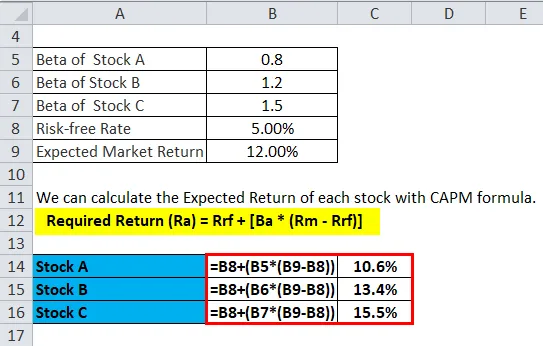
Le rendement attendu du projet est calculé comme suit:

La valeur nette de l'investissement est calculée comme suit:
Articles recommandés
Cela a été un guide pour une formule CAPM. Ici, nous discutons de ses utilisations ainsi que des exemples pratiques. Nous vous fournissons également CAPM Calculator avec un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Formule du ratio d'endettement
- Guide de la formule de rendement équivalent fiscal
- Exemples de formule prix / bénéfice
- Formule de retour sur l'actif moyen