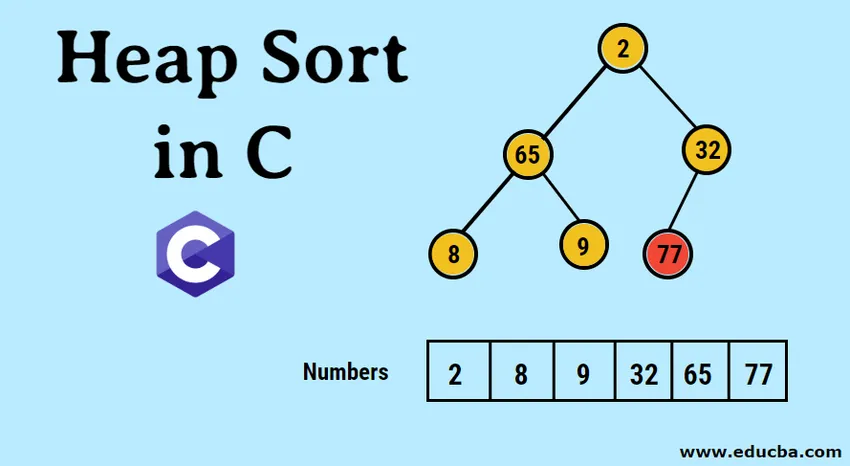
Introduction au tri en tas en C
Le tri est une technique qui consiste à classer les éléments en fonction de différentes propriétés. (Propriétés telles que l'organisation des données par ordre croissant, décroissant ou alphabétique). Un exemple majeur de tri auquel nous pouvons penser ici est la commande d'articles lors des achats en ligne. Nous pouvons nous référer aux prix, à la popularité, aux derniers et ainsi de suite. Il existe donc de nombreuses techniques pour ce positionnement d'éléments par tri. Dans cette rubrique, nous allons découvrir le tri de tas en C.
Ici, nous allons apprendre l'une des techniques de tri les plus courantes, Heap Sort, via le langage de programmation C.
La logique du tri par tas
Comment pouvons-nous réellement effectuer le tri en tas? Voyons ci-dessous.
Premièrement, le segment de mémoire est l'une des structures de données arborescentes. L'arbre impliqué ici est toujours un arbre binaire complet. Et, il existe deux types de tas
- Min - Tas: Généralement organisé dans l'ordre croissant, c'est-à-dire si l'élément de nœud parent a une valeur inférieure à celle des éléments de nœud enfant.
- Max - Heap: Généralement organisé en ordre décroissant, c'est-à-dire si l'élément de nœud parent a une valeur supérieure à celle des éléments de nœud enfant.
Étapes de tri du segment de mémoire
- Une fois les données de liste non triées obtenues, les éléments sont organisés dans la structure de données du tas en fonction de la création d'un tas min ou d'un tas max.
- Le premier élément de la liste ci-dessus est ajouté dans notre tableau
- La formation de la technique de structure de données de tête identique à celle de la première étape est à nouveau suivie et encore une fois, l'élément le plus élevé ou le plus petit élément est récupéré et ajouté dans notre tableau.
- Des étapes répétées nous aident à obtenir le tableau avec la liste triée.
Programme de tri de tas en C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Tout d'abord, nous demandons à l'utilisateur de saisir le nombre d'éléments qui sont pris pour le tri, puis l'utilisateur est autorisé à entrer différents éléments à trier.
Étapes suivies
- Le prochain sur lequel nous nous concentrons est de créer un tableau de tas, dans ce cas, un tableau de tas max.
- La condition principale pour obtenir un tableau max-heap est de vérifier qu'aucune valeur de nœud parent n'est inférieure à sa valeur de nœud enfant. Nous allons échanger jusqu'à ce que nous atteignions cette condition.
- Le principal avantage de cet arbre binaire complet est que les nœuds enfants gauche et droit d'un nœud parent sont accessibles avec les valeurs 2 (i) + 1 et 2 * (i) + 2 respectivement. Où i est le nœud parent.
- Donc, de cette façon ici, nous plaçons notre nœud racine qui contient la valeur maximale à l'endroit du nœud feuille le plus à droite. Et puis à nouveau en suivant la même procédure de sorte que le nombre maximal suivant devienne maintenant le nœud racine.
- Nous allons suivre la même procédure jusqu'à ce qu'il ne reste qu'un seul nœud dans le tableau de tas.
- Et puis, nous organisons notre tableau de tas pour former un tableau trié parfait dans l'ordre croissant.
- Enfin, nous imprimons le tableau trié dans la sortie.
Production:
La sortie est jointe ci-dessous.
Permettez-moi de vous montrer la représentation picturale des événements:
- Les données saisies sont d'abord représentées sous la forme d'un tableau unidimensionnel comme suit.

- La représentation picturale de l'arbre binaire formé est la suivante:
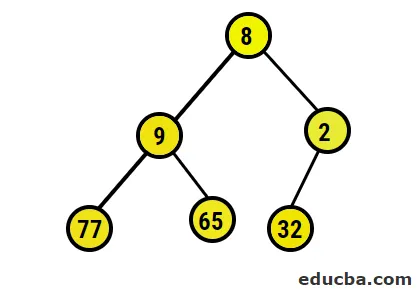
- Maintenant, nous allons convertir le tas max en nous assurant que tous les nœuds parents sont toujours supérieurs aux nœuds enfants. Comme mentionné dans la sortie sous tableau trié en tas, la représentation picturale serait:
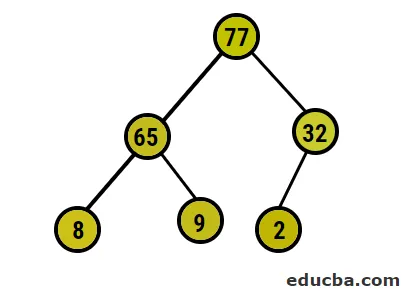
- Après cela, nous allons échanger le nœud racine avec le nœud feuille extrême, puis le supprimer de l'arborescence. Le nœud feuille serait de temps en temps la racine même processus e suivi pour obtenir à nouveau l'élément le plus élevé dans la racine
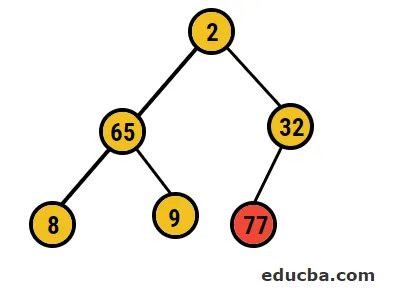
- Donc, dans ce cas, 77 chiffres sont supprimés de cet arbre et placés dans notre tableau trié et le processus est répété.
Ce qui précède, nous l'avons vu pour former un tableau de tas max. Le même processus est également traité avec la formation du réseau de min-tas. Comme indiqué ci-dessus, la seule différence réside dans la relation entre les éléments de nœud parent et enfant.
En tant qu'exercice, pouvez-vous essayer de former le tri de tas dans l'ordre décroissant?
Conclusion
Bien qu'il existe de nombreuses techniques de tri, le tri en tas est considéré comme l'une des meilleures techniques de tri en raison de sa complexité temporelle et spatiale. La complexité temporelle pour tous les meilleurs, moyens et pires cas est O (nlogn), où la pire des situations est meilleure que la pire des cas de Quicksort et la complexité de l'espace est O (1).
Articles recommandés
Ceci est un guide de tri de tas en C. Ici, nous discutons de la logique et des étapes du tri de tas avec l'exemple de code et la sortie ainsi que des représentations picturales. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Tri de tas en Java
- Tri de sélection en Java
- Palindrome en programme C
- Modèles en programmation C
- Tri de tas en C ++ (algorithme)
- Tri de tas en Python
- C Multiplication de la matrice de programmation