
Introduction aux fonctions dans R
La fonction est définie comme un ensemble d'instructions, pour effectuer et accomplir toute tâche logique spécifique. La fonction prend certains paramètres d'entrée qui sont connus comme des arguments pour effectuer cette tâche. Les fonctions aident à casser le code, en morceaux plus simples en l'orchestrant logiquement, ce qui est plus facile à lire et à comprendre. Dans cette rubrique, nous allons découvrir les fonctions de R.
Comment écrire des fonctions en R?
Pour écrire la fonction en R, voici la syntaxe:
Fun_name <- function (argument) (
Function body
)
Ici, on peut voir que le mot réservé spécifique "fonction" est utilisé dans R, pour définir n'importe quelle fonction. La fonction prend une entrée sous forme d'arguments. Le corps de la fonction est un ensemble d'instructions logiques qui sont effectuées sur des arguments, puis il renvoie la sortie. "Fun_name" est le nom donné à la fonction, à travers lequel elle peut être appelée n'importe où dans le programme R.
Voyons un exemple, qui sera plus lucide pour comprendre le concept de fonction dans R.
Code R
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
production:
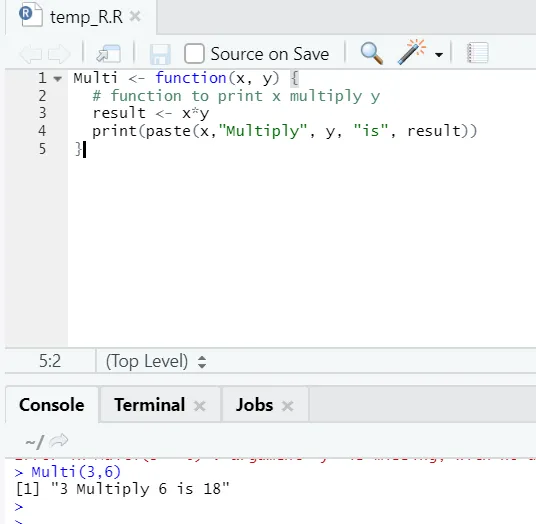
Ici, nous avons créé le nom de la fonction «Multi», qui prend deux arguments en entrée et fournit la sortie multipliée. Le premier argument est x et le deuxième argument est y. Comme vous pouvez le voir, nous avons appelé la fonction par le nom «Multi». Ici, si quelqu'un le souhaite, les arguments peuvent également être définis sur la valeur par défaut.
Différents types de fonctions dans R
Différentes fonctions R avec syntaxe et exemples (intégrés, mathématiques, statistiques, etc.)
1) Fonction intégrée -
Ce sont les fonctions fournies avec R pour répondre à une tâche spécifique en prenant un argument en entrée et en donnant une sortie basée sur l'entrée donnée. Discutons ici quelques fonctions générales importantes de R:
a) Tri: les données peuvent être triées par ordre croissant ou décroissant. Les données peuvent être soit un vecteur de variable continue, soit une variable factorielle.
Syntaxe:

Voici l'explication de ses paramètres:
- x: il s'agit d'un vecteur de la variable continue ou variable factorielle
- décroissant: cela peut être défini sur Vrai / Faux pour contrôler l'ordre par ascendant ou descendant. Par défaut, c'est FAUX ».
- last: si le vecteur a des valeurs NA, doit-il être mis en dernier ou non
Code R et sortie:
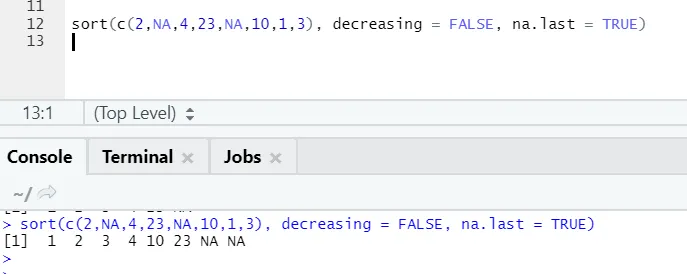
Ici, on peut remarquer comment les valeurs «NA» s'alignent à la fin. Comme notre paramètre na.last = True était vrai.
b) Seq: il génère une séquence du nombre entre deux nombres spécifiés.
Syntaxe
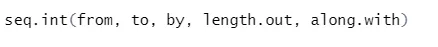
Voici l'explication de ses paramètres:
- from, pour démarrer et terminer la valeur de la séquence.
- par: Incrément / écart entre deux nombres consécutifs dans la séquence
- length.out: la longueur requise de la séquence.
- Along.with: fait référence à la longueur de la longueur de cet argument
Code R et sortie:
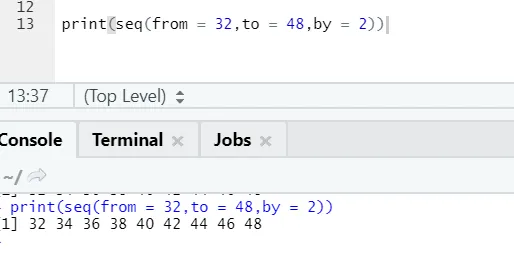
Ici, on peut remarquer que la séquence générée a une incrémentation de 2 car par est défini comme 2.
c) Toupper, tolower: Les deux fonctions: toupper et tolower sont des fonctions appliquées sur la chaîne pour changer la casse des lettres dans les phrases.
Code R et sortie:
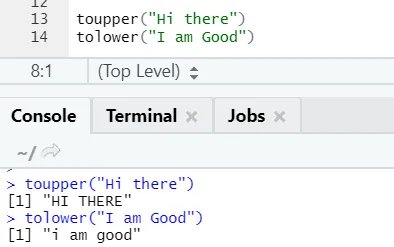
On peut remarquer comment les majuscules et les minuscules changent lorsqu'elles sont appliquées à la fonction.
d) Rnorm: il s'agit d'une fonction intégrée qui génère des nombres aléatoires.
Code R et sortie:
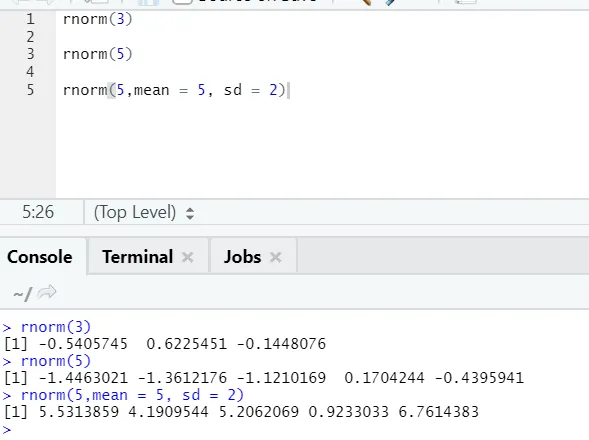
La fonction rnorm prend le premier argument qui indique combien de nombres doivent être générés.
e) Rep: Cette fonction réplique la valeur autant de fois que spécifié.
Syntaxe R: rnorm (x, n)
Ici, x représente la valeur à répliquer et n représente le nombre de fois qu'il doit être répliqué.
Code R et sortie:
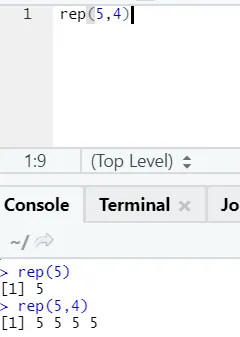
f) Coller: Cette fonction consiste à concaténer des chaînes avec un caractère spécifique entre les deux.
syntaxe
paste(x, sep = “”, collapse = NULL)
Code R
paste("fish", "water", sep=" - ")
Sortie R:
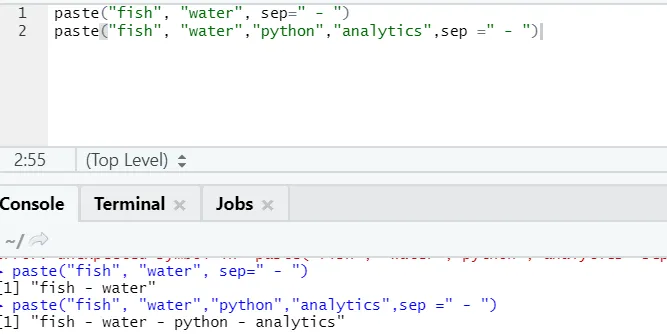
Comme vous pouvez le voir, nous pouvons également coller plus de deux chaînes. Sep est ce caractère spécifique que nous avons ajouté entre les chaînes. Par défaut, sep est l'espace.
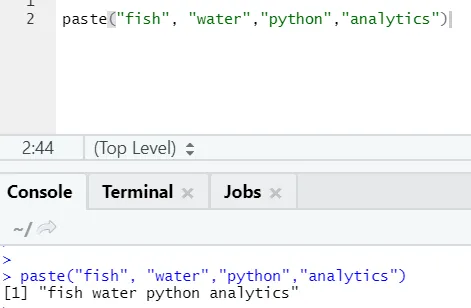
Une autre fonction similaire existe comme celle-ci, dont tout le monde devrait être conscient est paste0.
La fonction paste0 (x, y, collapse) fonctionne de manière similaire à paste (x, y, sep = “”, collapse)
Veuillez voir l'exemple ci-dessous:
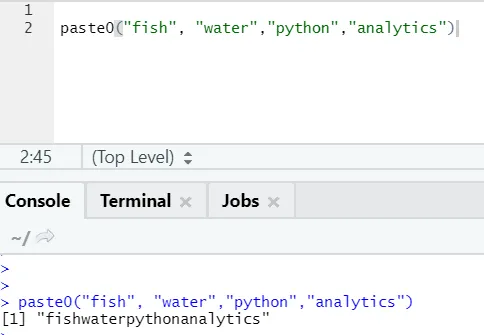
En termes simples, pour résumer coller et coller0:
Coller0 est plus rapide que coller quand il s'agit de la concaténation de chaînes sans séparateur. Comme coller recherche toujours «sep» et qui est de l'espace par défaut.
g) Strsplit: Cette fonction consiste à diviser la chaîne. Voyons les cas simples:
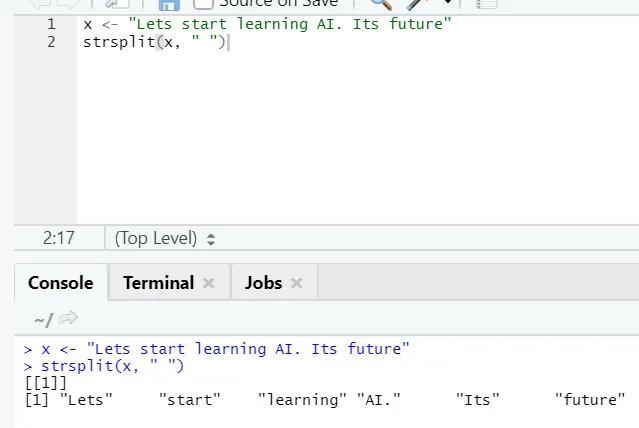
h) Rbind: La fonction rbind aide à combiner les vecteurs avec le même nombre de colonnes, l'une sur l'autre.
Exemple
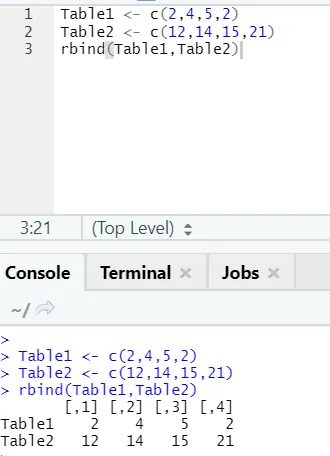
i) cbind: il combine des vecteurs avec le même nombre de lignes, côte à côte.
Exemple
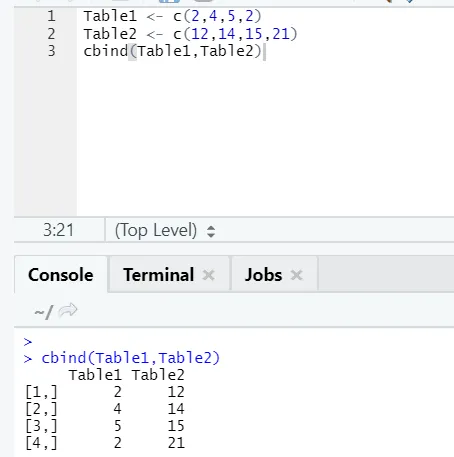
Si le nombre de lignes ne correspond pas, voici l'erreur que vous trouverez:

Cbind et rbind aident à la manipulation et au remodelage des données.
2) Fonction mathématique -
R fournit une grande variété de fonctions mathématiques. Voyons-en quelques-uns en détail:
a) Sqrt: Cette fonction calcule la racine carrée d'un nombre ou d'un vecteur numérique.
Code R et sortie:
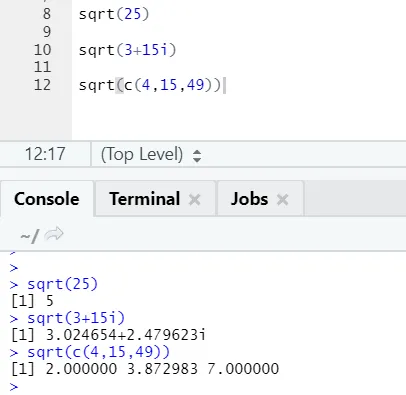
On peut voir comment calculer la racine carrée d'un nombre, un nombre complexe et une séquence de vecteur numérique a été calculée.
b) Exp: Cette fonction calcule la valeur exponentielle d'un nombre ou d'un vecteur numérique.
Code R et sortie:
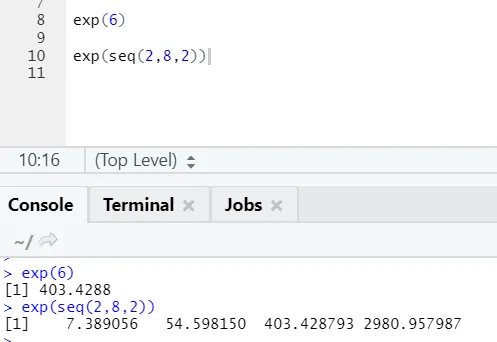
c) Cos, Sin, Tan: Ce sont des fonctions de trigonométrie implémentées dans R ici.
Code R et sortie:
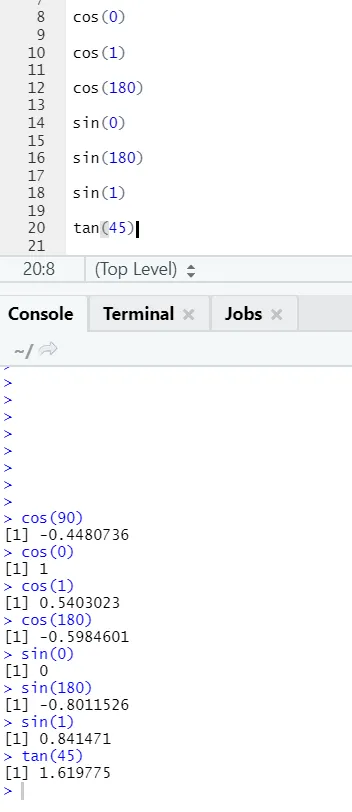
d) Abs: Cette fonction renvoie la valeur positive absolue d'un nombre.
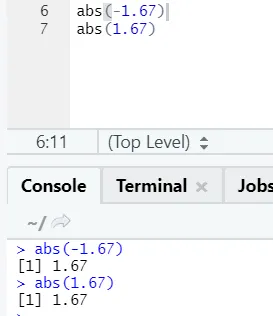
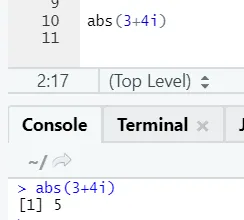
Comme vous pouvez le voir, le négatif ou le positif d'un nombre sera retourné dans sa forme absolue. Voyons cela pour un nombre complexe:
e) Journal: Il s'agit de trouver le logarithme d'un nombre.
Voici l'exemple ci-dessous:
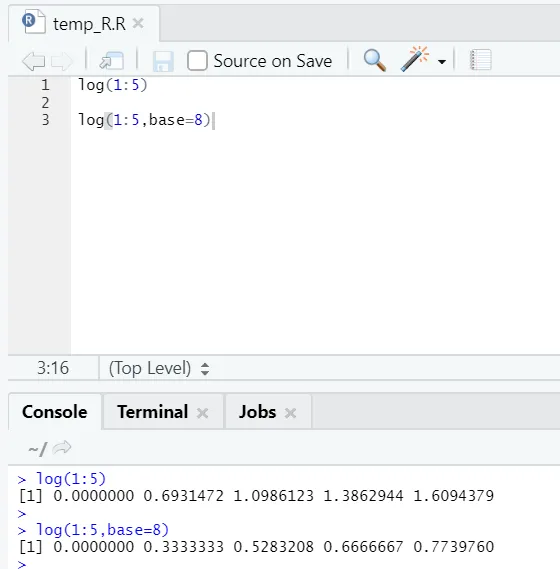
Ici, on obtient la flexibilité de changer la base, selon l'exigence.
f) Cumsum: Il s'agit d'une fonction mathématique qui donne des sommes cumulées. Voici l'exemple ci-dessous:
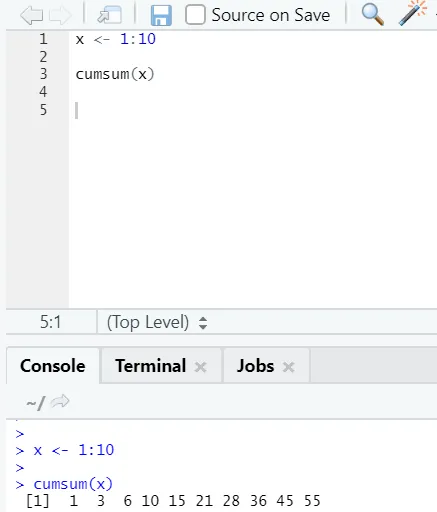
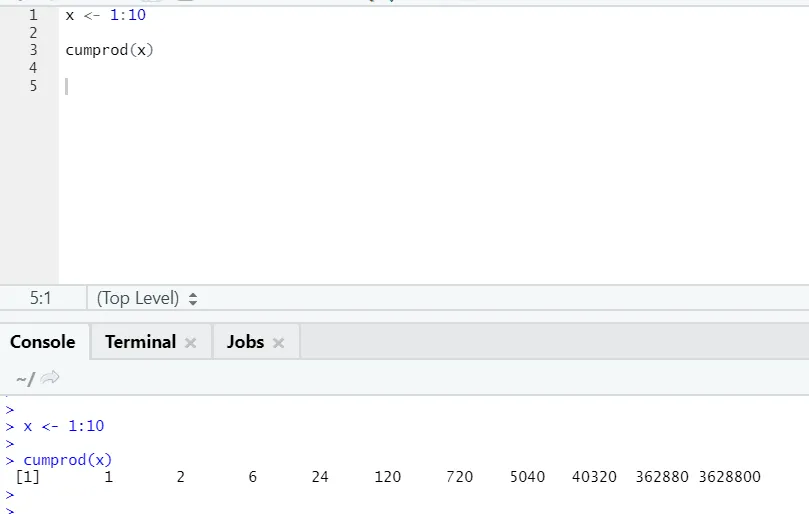
g) Cumprod: Comme la fonction mathématique Cumsum, nous avons cumprod où la multiplication cumulative se produit.
Veuillez voir l'exemple ci-dessous:
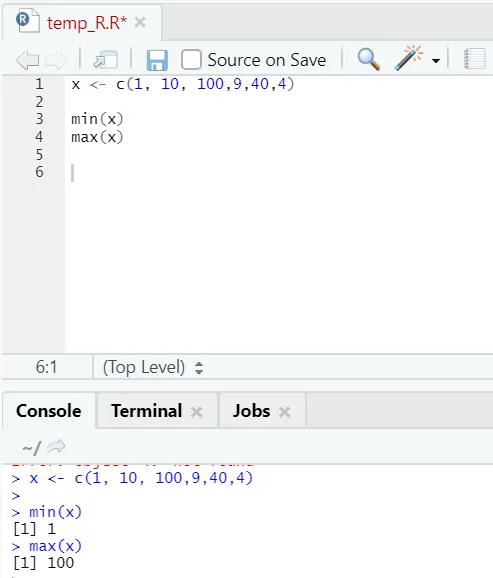
h) Max, Min: Cela vous aidera à trouver la valeur maximale / minimale dans l'ensemble de nombres. Voir ci-dessous les exemples liés à cela:
i) Plafond: Le plafond est une fonction mathématique qui renvoie le plus petit de l'entier supérieur à celui spécifié.
Regardons un exemple:
plafond (2.67)
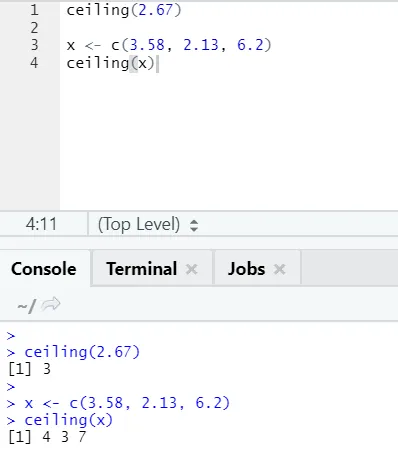
Comme vous pouvez le constater, le plafond est appliqué sur un nombre ainsi que sur une liste, et la sortie est le plus petit de l'entier supérieur suivant.
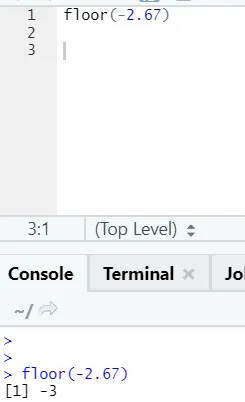
j) Étage: l'étage est une fonction mathématique qui renvoie le plus petit nombre entier du nombre spécifié.
L'exemple ci-dessous vous aidera à mieux le comprendre:
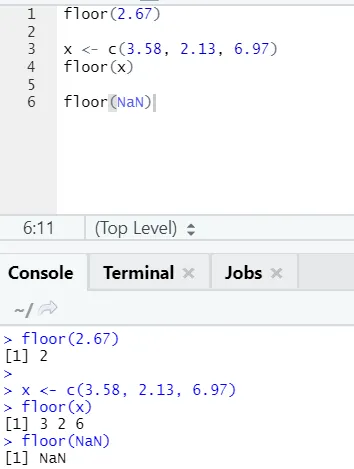
Il en va de même pour les valeurs négatives. S'il vous plaît, jetez un oeil:
3) Fonctions statistiques -
Ce sont les fonctions qui décrivent la distribution de probabilité associée.
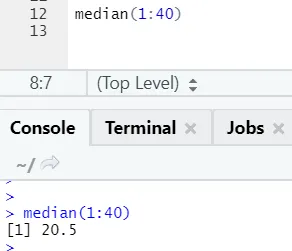
a) Médiane: Ceci a calculé la médiane à partir de la séquence de nombres.
Syntaxe
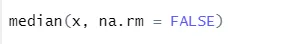
Code R et sortie:
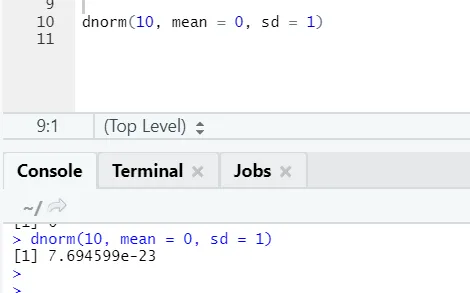
b) Dnorm: il s'agit de la distribution normale. La fonction dnorm renvoie la valeur de la fonction de densité de probabilité, pour la distribution normale des paramètres donnés pour x, μ et σ.
Code R et sortie:
c) Cov: la covariance indique si deux vecteurs sont positivement, négativement ou totalement non liés.
Code R
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Sortie R:
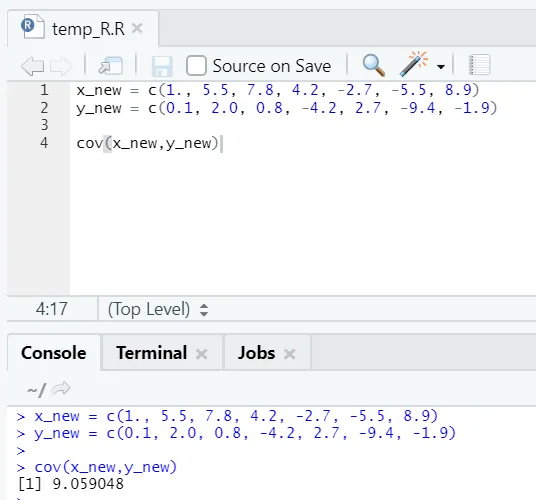
Comme vous pouvez le voir, deux vecteurs sont liés positivement, ce qui signifie que les deux vecteurs se déplacent dans la même direction. Si la covariance est négative, cela signifie que x et y sont inversement liés et se déplacent donc dans la direction opposée.
d) Cor: C'est une fonction pour trouver la corrélation entre les vecteurs. Il donne en fait le facteur d'association entre les deux vecteurs qui est connu comme le «coefficient de corrélation». La corrélation ajoute un facteur de degré à la covariance. Si deux vecteurs sont positivement corrélés, la corrélation vous indiquera également dans quelle mesure ils sont positivement liés.
Ces trois types de méthodes qui peuvent être utilisées pour trouver une corrélation entre deux vecteurs:
- Corrélation de Pearson
- Corrélation de Kendall
- Corrélation de Spearman
Au format R simple, cela ressemble à:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Ici x et y sont des vecteurs.
Voyons l'exemple pratique de la corrélation sur un ensemble de données intégré.
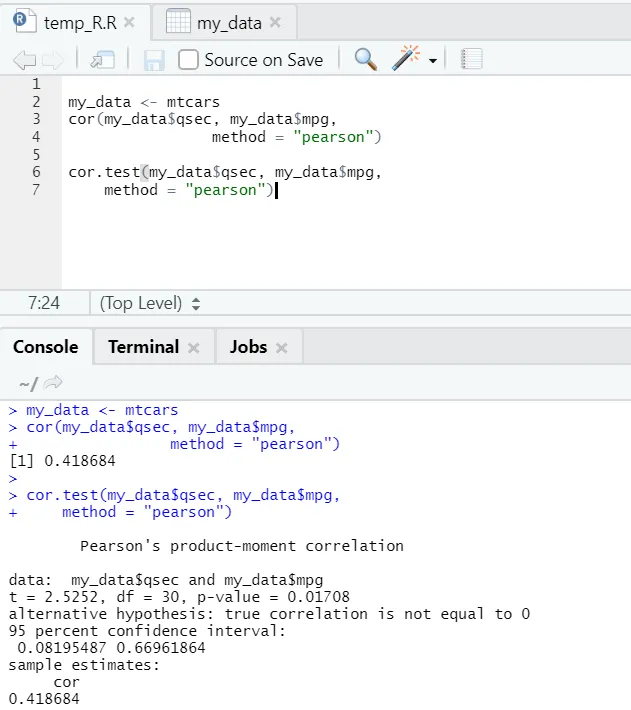
Donc, ici vous pouvez voir que la fonction «cor ()» a donné le coefficient de corrélation 0, 41 entre «qsec» et «mpg». Cependant, une autre fonction a également été présentée, à savoir «cor.test ()» qui indique non seulement le coefficient de corrélation, mais aussi la valeur p et la valeur t qui lui sont associées. L'interprétation devient beaucoup plus facile avec la fonction cor.test.
On peut faire la même chose avec les deux autres méthodes de corrélation:
Code R pour la méthode Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Code R pour la méthode Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Code R pour la méthode Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Le coefficient de corrélation se situe entre -1 et 1.
Si le coefficient de corrélation est négatif, cela implique que lorsque x augmente, y diminue.
Si le coefficient de corrélation est nul, cela implique qu'il n'existe aucune association entre x et y.
Si le coefficient de corrélation est positif, cela implique que lorsque x augmente, y tend également à augmenter.
e) Test T: Le test T vous dira si deux ensembles de données proviennent des mêmes distributions normales (en supposant) ou non.
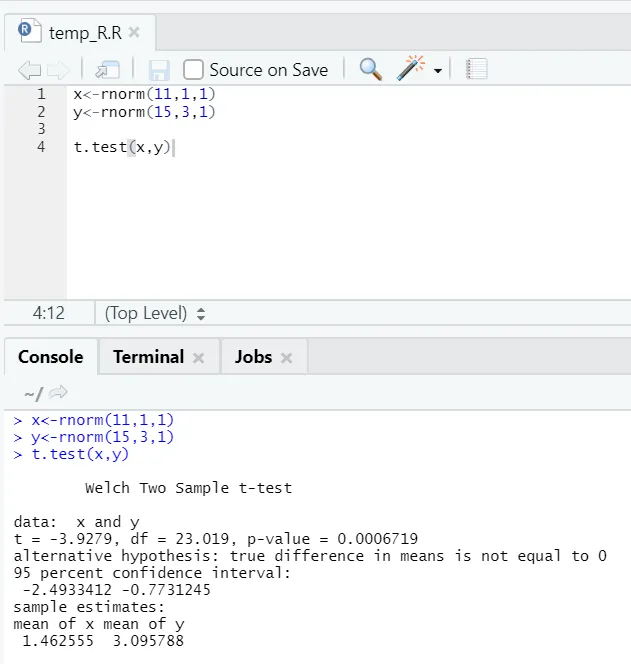
Ici, vous devez rejeter l'hypothèse nulle selon laquelle les deux moyennes sont égales car la valeur de p est inférieure à 0, 05.
Cette instance affichée est de type: ensembles de données non appariés avec des variances inégales. De même, peut être essayé avec l'ensemble de données apparié.
f) Régression linéaire simple: elle montre la relation entre la variable prédictive / indépendante et la réponse / la variable dépendante.
Un exemple pratique simple pourrait être de prédire le poids d'une personne si sa taille est connue.
Syntaxe R
lm(formula, data)
Ici, la formule décrit la relation entre la sortie, c'est-à-dire y et la variable d'entrée iex. Les données représentent l'ensemble de données sur lequel la formule doit être appliquée.
Voyons un exemple pratique, où la surface au sol est la variable d'entrée et le loyer est la variable de sortie.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
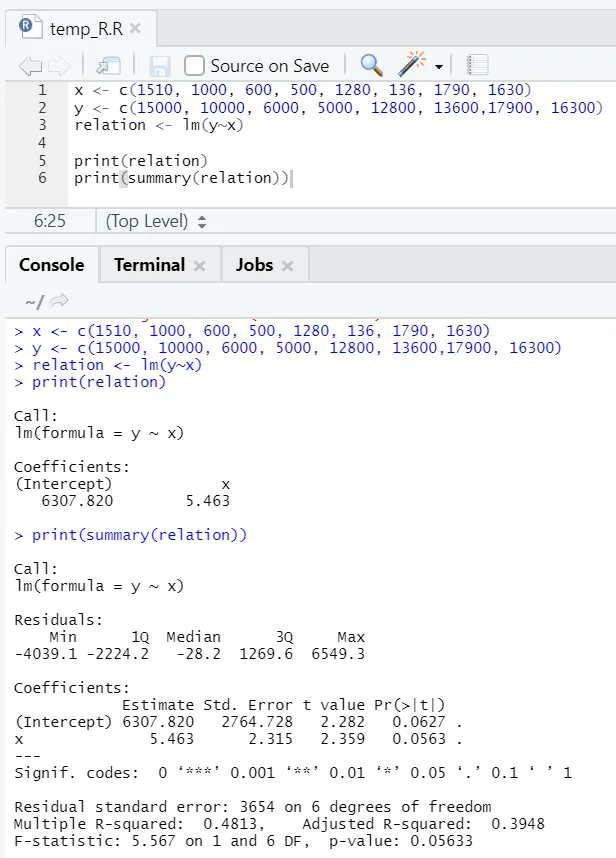
Ici, la valeur P n'est pas inférieure à 5%. L'hypothèse nulle ne peut donc pas être rejetée. Il n'y a pas beaucoup d'importance pour prouver la relation entre la surface de plancher et le loyer.
Ici, la valeur du carré R est de 0, 4813. Cela implique que seulement 48% de la variance dans la variable de sortie peut être expliquée par la variable d'entrée.
Disons maintenant que nous devons prédire une valeur de surface au sol, sur la base du modèle ci-dessus.
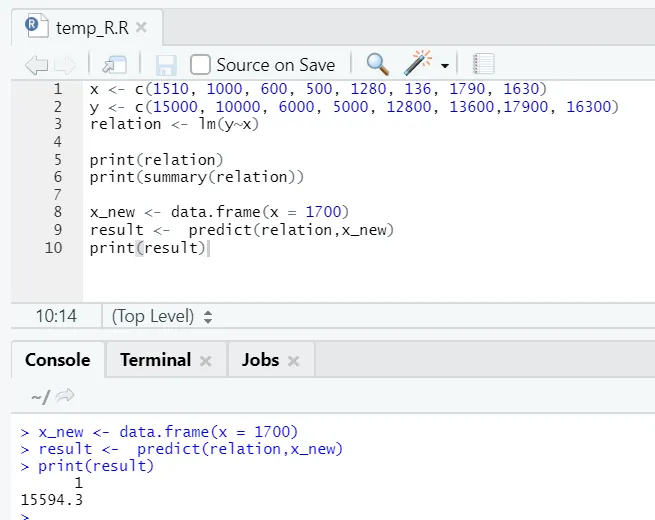
Code R
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Sortie R:
Après l'exécution du code R ci-dessus, la sortie ressemblera à ceci:
On peut adapter et visualiser la régression. Voici le code R pour cela:
# Donnez un nom au fichier graphique png.
png(file = "LinearRegressionSample.png.webp")
# Tracer le graphique.
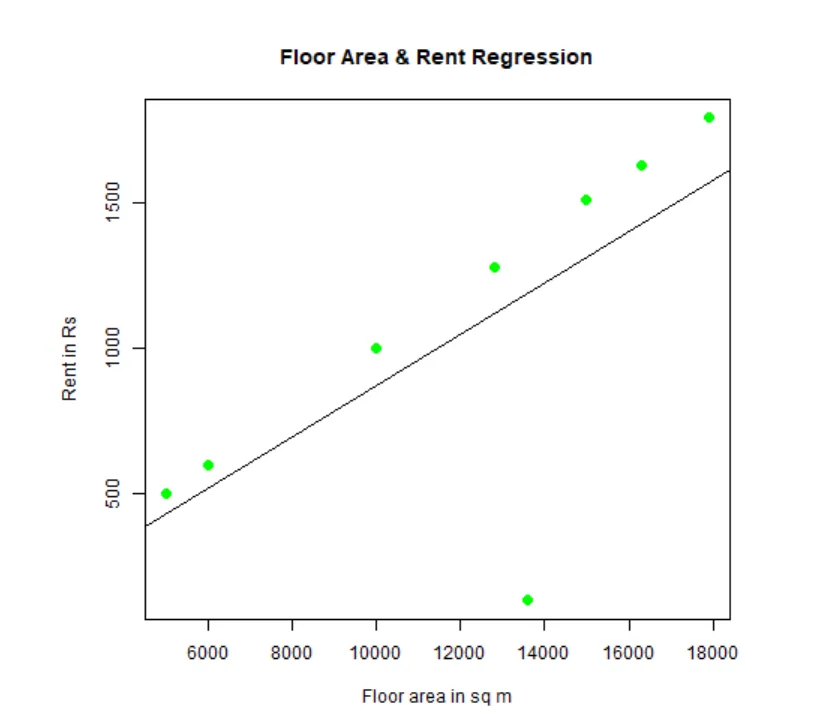
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Enregistrez le fichier.
dev.off()
Ce graphique «LinearRegressionSample.png.webp» sera généré dans votre répertoire de travail actuel.
g) Test du chi carré
Il s'agit d'une fonction statistique dans R. Ce test conserve sa signification afin de prouver s'il existe une corrélation entre deux variables catégorielles.
Ce test fonctionne également comme tout autre test statistique basé sur la valeur de p, on peut accepter ou rejeter l'hypothèse nulle.
Syntaxe R
chisq.test(data), /code>
Voyons-en un exemple pratique.
Code R
# Chargez la bibliothèque.
library(datasets)
data(iris)
# Créez un bloc de données à partir de l'ensemble de données principal.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Créez un tableau avec les variables nécessaires.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Effectuez le test du chi carré.
print(chisq.test(iris.data))
Sortie R:
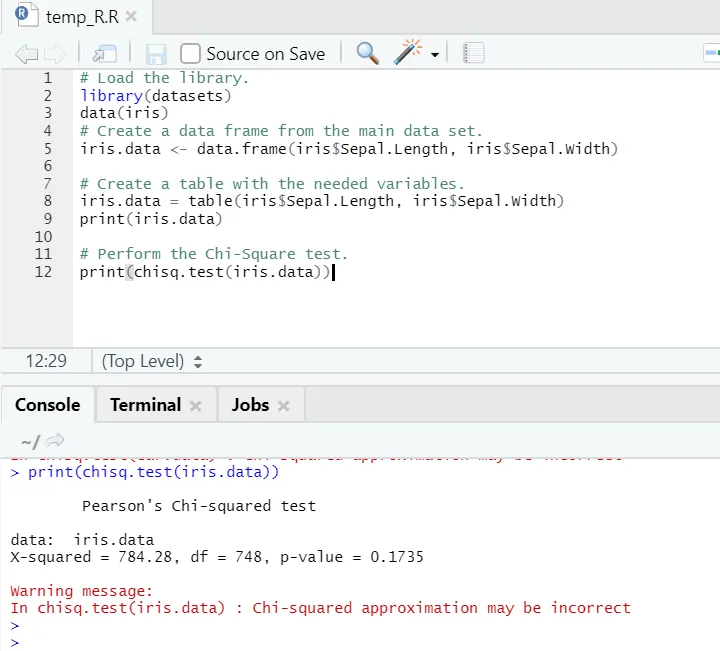
Comme on peut le voir, le test du chi carré a été effectué sur un ensemble de données iris, en considérant ses deux variables «Sepal. Longueur "et" Sepal.Width ".
La valeur de p n'est pas inférieure à 0, 05, il n'y a donc pas de corrélation entre ces deux variables. Ou nous pouvons dire que ces deux variables ne sont pas dépendantes l'une de l'autre.
Conclusion
Les fonctions de R sont simples, faciles à installer, faciles à saisir et pourtant très puissantes. Nous avons vu une variété de fonctions qui sont utilisées dans le cadre des bases de R. Une fois que l'on se familiarise avec ces fonctions discutées ci-dessus, on peut explorer d'autres variétés de fonctions. Les fonctions vous aident à faire fonctionner votre code de manière simple et concise. Les fonctions peuvent être intégrées ou définies par l'utilisateur, tout dépend du besoin tout en résolvant un problème. Les fonctions donnent une bonne forme à un programme.
Articles recommandés
Ceci est un guide des fonctions dans R. ici, nous discutons comment écrire des fonctions dans R et différents types de fonctions dans R avec la syntaxe et des exemples. Vous pouvez également consulter l'article suivant pour en savoir plus -
- Fonctions de chaîne R
- Fonctions de chaîne SQL
- Fonctions de chaîne T-SQL
- Fonctions de chaîne PostgreSQL