Nombres complexes dans MATLAB - Comment générer un nombre complexe?

Introduction aux nombres complexes dans MATLAB

Les nombres complexes sont la combinaison de nombres réels et de nombres imaginaires sous la forme de p + qi où p et q sont les nombres réels et i est le nombre imaginaire. Un nombre imaginaire est défini où i est le résultat d'une équation a 2 = -1. Nous pouvons utiliser i ou j pour désigner les unités imaginaires. Comme les nombres complexes sont utilisés dans tous les calculs mathématiques, Matlab est principalement utilisé pour effectuer des calculs mathématiques. Ainsi, les nombres complexes constituent une partie importante de l'apprentissage de Matlab.

Génération de nombres complexes dans MATLAB

Les numéros complexes peuvent être créés ou déclarés dans Matlab à l'aide d'une fonction «complexe». Nous pouvons également créer des nombres complexes en trouvant la racine carrée de tout nombre négatif. Dans Matlab, nous pouvons utiliser i ou j pour désigner la partie imaginaire du nombre complexe.

Exemples

X = 4 + 5i

Ici, X est un nombre complexe qui contient 2 parties, c'est-à-dire une partie réelle et une partie imaginaire. 4 est la partie réelle et 5 est la partie imaginaire. Nous pouvons trouver les parties réelles et imaginaires en utilisant des fonctions dans Matlab.

a = réel (X) = 4 (Cela donne la partie réelle du nombre complexe)
b = imag (X) = 5 (Cela donne la partie imaginaire du nombre complexe)
complexe (6, 7) = 6 + 7i (Cette fonction est utilisée pour créer un nombre complexe)

Nous pouvons également créer des tableaux complexes dans Matlab qui peuvent également être déclarés à l'aide des fonctions complexes.

a = complexe (x, y)

Il y a certaines conditions pour x et y que nous devons suivre comme x et y ne doivent pas être simples ou doubles. Un scalaire complexe peut être créé si deux entrées sont de nature scalaire comme,

X = complexe (5, 3)
X = 5.0000 + 3.0000i

De même, un vecteur complexe peut être créé si nous avons deux entrées comme vecteurs.

X = uint8 ((4; 5; 6; 7));
Y = uint8 ((3; 5; 1; 2));
a = complexe (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Nous pouvons créer un nombre complexe ayant un seul scalaire comme,

X = complexe (10)
X = 10, 0000 + 0, 0000i

Il y a certaines conditions que les arguments d'entrée et de sortie doivent suivre comme,

Les arguments d'entrée contiennent des parties réelles et imaginaires comme x any y. x et y doivent être scalaires, vectoriels, matriciels multidimensionnels ou matriciels dans MATLAB. Les tailles x et y doivent être identiques. Ils doivent être du même type de données, mais il y a quelques exceptions comme double peut être utilisé avec simple et entier peut être combiné avec un double qui est scalaire.

La sortie du tableau peut être vectorielle, scalaire, matricielle ou multidimensionnelle en fonction des arguments d'entrée. La taille de la sortie doit être la même que celle de l'entrée. Si les arguments d'entrée sont de types de données différents de ceux déterminés par la sortie,

Si l'un des arguments d'entrée est de nature unique, la sortie doit également être unique.
Si l'un des arguments d'entrée est de nature entière, la sortie doit être d'un type de données entier.

Nous pouvons vérifier si la matrice est réelle ou imaginaire en utilisant la fonction isreal.

Code:

X = (2+i, 1); Isreal(X)

Production:

Code:

Isreal (X (2))

Production:

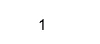
Pour extraire les parties réelles et imaginaires, nous pouvons utiliser des fonctions réelles et imagées dans Matlab comme,

Code:

real(X)

Production:

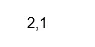
Code:

imag(X)

Production:

Opérations et fonctions des nombres complexes dans MATLAB

Il y a plusieurs opérations et fonctions qui peuvent être effectuées en utilisant des nombres complexes dans Matlab comme

abs: Cette fonction est utilisée pour trouver le module de tout nombre complexe sous la forme de p + qi. abs (2 + 3i) = racine carrée de (2 2 + 3 2) = (13) 0, 5
angle: pour trouver l'angle de phase du nombre complexe.

Il y a certains conseils qui devraient être suivis pour le bon fonctionnement des nombres complexes dans Matlab comme,

Nous devons éviter d'utiliser i et j comme partie de tout nom de variable car ils sont utilisés pour désigner les parties imaginaires du nombre complexe.
Nous devons éviter d'utiliser j ou i si la partie imaginaire est 1. Au lieu de cela, nous pouvons utiliser 1j ou 1i.
Nous pouvons créer une fonction complexe dans Matlab lorsque i et j sont utilisés comme noms de variables dans une partie, les arguments d'entrée ne sont pas de type simple ou double et la partie imaginaire est nulle.

Conclusion

Les nombres complexes sont utilisés dans le domaine mathématique ou technique. De nombreuses applications réelles ou pratiques peuvent être décrites en utilisant la partie imaginaire de nombres complexes. Il est donc important de comprendre l'utilisation et les applications des nombres complexes dans diverses plates-formes, surtout si vous traitez avec n'importe quel domaine physique ou mathématique.

Articles recommandés

Ceci est un guide des nombres complexes dans MATLAB. Nous discutons ici de l'introduction et de la génération de nombres complexes dans matlab, y compris ses exemples avec opération et fonction. Vous pouvez également consulter les articles suivants pour en savoir plus-