Introduction à l' arborescence AVL dans la structure de données
L'arbre AVL dans la structure de données fait référence à l'arbre Adelson, Velski et Landis. Il s'agit d'une version améliorée de l'arborescence de recherche binaire. Il a toutes les fonctionnalités de l'arbre de recherche binaire, mais ne diffère que par le fait qu'il maintient une différence entre la hauteur du sous-arbre gauche et du sous-arbre droit et assure également que sa valeur est <= 1 dans l'arbre, c'est ce qu'on appelle la balance Facteur.
Balance Factor = height(left-subtree) − height(right-subtree)
Par exemple: Considérez les arbres suivants

Dans l'exemple ci-dessus, la hauteur du sous-arbre droit = 2 et gauche = 3 donc BF = 2 qui est <= 1 donc l'arbre est dit équilibré.
Pourquoi avons-nous besoin d'une arborescence AVL dans DS?
En travaillant avec l'arbre de recherche binaire, nous rencontrons un scénario où les éléments sont triés. Dans de tels cas, tous les éléments du tableau sont disposés sur un côté de la racine, ce qui entraîne une augmentation de la complexité temporelle de la recherche d'un élément dans un tableau et la complexité devient -O (n), c'est-à-dire la pire des situations de l'arbre . Pour résoudre ces problèmes et réduire le temps de recherche, les arbres AVL ont été inventés par Adelson, Velski & Landis.
Exemple:

Dans la figure ci-dessus, la hauteur du sous-arbre gauche = 3 était comme
Hauteur du sous-arbre droit = 0
Ainsi, le facteur d'équilibre = 3-0 = 3. Ainsi, la recherche d'un élément dans un tel arbre a O (n) de complexité qui est similaire à la recherche linéaire. Pour éviter cette recherche complexe, l'arborescence AVL a été introduite là où chaque nœud de l'arborescence doit être maintenu
facteur d'équilibre <= 1, sinon diverses techniques de rotation doivent être effectuées pour équilibrer cet arbre.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Types de rotations
Lorsque le facteur d'équilibre de l'arbre ne satisfait pas à la condition <= 1, des rotations doivent alors être effectuées sur lui pour le transformer en arbre équilibré.
Il existe 4 types de rotations:
1. Rotation à gauche: si l'ajout d'un nœud à droite de l'arborescence entraîne un déséquilibre, dans ce cas, la rotation à gauche doit être effectuée.
2. Rotation à droite: si l'ajout d'un nœud à gauche de l'arborescence entraîne un déséquilibre du nœud, la rotation à droite doit être effectuée. En d'autres termes, lorsque le nombre de nœuds augmente sur le côté gauche, il apparaît un besoin de déplacer les éléments vers le côté droit pour l'équilibrer ainsi, il est dit que c'est la rotation à droite.
3. Rotation gauche-droite: Ce type de rotation est une combinaison des 2 rotations ci-dessus expliquées. Ce type de rotation se produit lorsqu'un élément est ajouté au sous-arbre droit d'un arbre gauche.
Dans un tel cas, effectuez d'abord une rotation à gauche sur le sous-arbre, suivie d'une rotation à droite de l'arbre de gauche.
4. Rotation droite-gauche: ce type de rotation est également composé d'une séquence de plus de 2 rotations. Ce type de rotation est nécessaire lorsqu'un élément est ajouté à gauche du sous-arbre droit et que l'arbre devient déséquilibré. Dans un tel cas, nous effectuons d'abord une rotation à droite sur le sous-arbre droit, puis une rotation à gauche sur l'arbre de droite.
Opérations sur l'arborescence AVL dans DS
Ci-dessous 3 opérations qui peuvent être effectuées sur l'arborescence AVL: -
1. Recherche
Cette opération est similaire à l'exécution d'une recherche dans l'arborescence de recherche binaire. Les étapes suivies sont les suivantes:
- Lisez l'élément fourni par l'utilisateur disons x.
- Comparez l'élément de la racine, s'il est le même, quittez sinon passez à l'étape suivante.
- Si x
Sinon, allez vers le bon enfant et comparez à nouveau.
Suivez les processus B et C jusqu'à ce que vous trouviez l'élément et quittez.
Ce processus a une complexité O (log n).
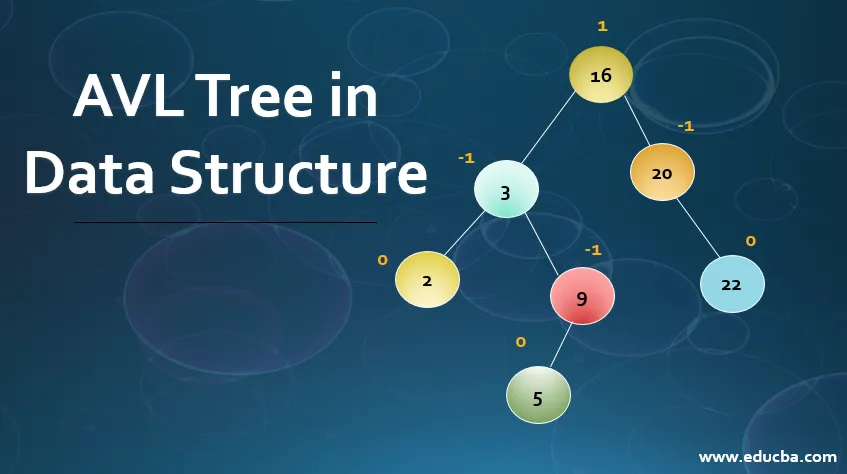
Exemple:
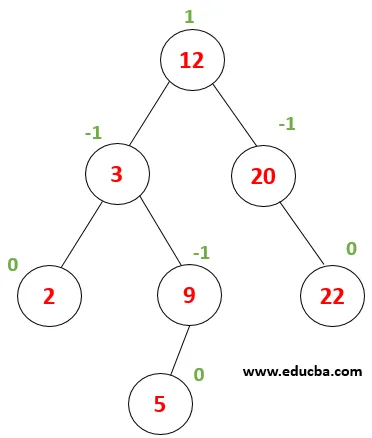 | Considérez cet arbre, où nous devons effectuer une recherche pour la valeur de nœud 9. Soit d'abord x = 9, valeur racine (12)> x puis, la valeur doit être dans le sous-arbre gauche de l'élément racine. |
 | Maintenant, x est comparé à la valeur du nœud 3 x> 3 nous devons donc aller vers le sous-arbre droit. |
 | Maintenant, x est comparé au nœud (9), où 9 == 9 renvoie vrai. Ainsi, la recherche d'éléments se termine dans l'arborescence. |
2. Insertion
Lors de l'insertion d'un élément dans l'arborescence AVL, nous devons trouver l'emplacement particulier de l'élément qui doit être inséré, puis l'élément est attaché de la même manière qu'une insertion dans BST mais après cela, il est vérifié si l'arborescence est toujours équilibrée ou non c'est-à-dire que le facteur d'équilibre d'un nœud est <= 1. Et des rotations particulières sont effectuées selon les besoins.
La complexité est O (log n).
Exemple: considérez l'arborescence ci-dessous,
 | Chaque nœud a un facteur d'équilibre de 0, -1 ou 1, donc l'arbre est équilibré. Permet maintenant ce qui se passe lorsqu'un nœud de valeur 1 est inséré. Le premier arbre est parcouru pour trouver l'emplacement où il doit être inséré… 1 <2 s'écrit donc comme un enfant gauche du nœud (2). |
 | Après insertion, le nœud (9) devient déséquilibré avec un facteur d'équilibre = 2. Il est maintenant soumis à subir une rotation à droite. |
 | Un arbre devient équilibré après la rotation à droite et l'opération d'insertion est ainsi terminée avec succès. |
3. Suppression
La suppression d'un élément dans l'arborescence AVL comprend également la recherche d'un élément dans l'arborescence, puis sa suppression. L'opération de recherche est la même que BST, et après avoir trouvé l'élément à supprimer, l'élément est supprimé de l'arborescence et les éléments sont ajustés pour le rendre à nouveau BST. Après ces éléments sont vérifiés pour avoir un facteur d'équilibre de 0, -1 ou 1 et donc des rotations appropriées sont effectuées pour le rendre équilibré.
Complexité si O (log n).
 | Considérons l'arbre donné, dont tous ont un facteur d'équilibre de 0, -1 ou 1. Supprimons maintenant un nœud de valeur 16. Le premier arbre est parcouru pour trouver le nœud de valeur 16 identique à un algorithme de recherche. |
 | Le nœud 16 sera remplacé par le prédécesseur en ordre de ce nœud qui est le plus grand élément du sous-arbre gauche, c'est-à-dire 12 L'arbre est devenu déséquilibré donc LL - une rotation doit être effectuée. |
 | Maintenant, chaque nœud est devenu équilibré. |
Conclusion - Arbre AVL dans la structure des données
L'arbre AVL est un descendant de l'arbre de recherche binaire mais surmonte son inconvénient de complexité croissante au cas où les éléments seraient triés. Il surveille le facteur d'équilibre de l'arbre à 0 ou 1 ou -1. Dans le cas où l'arbre devient déséquilibré, des techniques de rotation correspondantes sont effectuées pour équilibrer l'arbre.
Articles recommandés
Ceci est un guide de l'arborescence AVL dans la structure de données. Nous discutons ici de l'introduction, des opérations sur l'arborescence AVL dans DS et des types de rotations. Vous pouvez également consulter nos autres articles connexes pour en savoir plus–
- Éléments jQuery
- Qu'est-ce que la science des données
- Types d'arbres dans la structure de données
- Types de données C #