Différence entre la régression linéaire et la régression logistique
L'article suivant régression linéaire vs régression logistique fournit les différences les plus importantes entre les deux, mais avant de voir ce que signifie la régression?
Régression
La régression est fondamentalement une mesure statistique pour déterminer la force de la relation entre une variable dépendante, c'est-à-dire la sortie Y, et une série d'autres variables indépendantes, c'est-à-dire X 1, X 2, etc. L'analyse de régression est essentiellement utilisée pour la prédiction et la prévision.
Qu'est-ce que la régression linéaire?
La régression linéaire est un algorithme basé sur le domaine d'apprentissage supervisé de l'apprentissage automatique. Il hérite d'une relation linéaire entre ses variables d'entrée et la variable de sortie unique lorsque la variable de sortie est de nature continue. Il est utilisé pour prédire la valeur de la sortie, disons Y à partir des entrées, disons X. Lorsqu'une seule entrée est considérée, elle est appelée régression linéaire simple.
Il peut être classé en deux catégories principales:
1. Régression simple
Principe de fonctionnement: L'objectif principal est de trouver l'équation d'une droite qui correspond le mieux aux données échantillonnées. Cette équation décrit algébriquement la relation entre les deux variables. La ligne droite la mieux ajustée est appelée ligne de régression.
Y = β 0 + β 1 X
Où,
β représente les caractéristiques
β 0 représente l'ordonnée à l'origine
β 1 représente le coefficient de la caractéristique X
2. Régression multivariable
Il est utilisé pour prédire une corrélation entre plusieurs variables indépendantes et une variable dépendante. La régression avec plus de deux variables indépendantes est basée sur l'ajustement de la forme à la constellation de données sur un graphique multidimensionnel. La forme de régression doit être telle qu'elle minimise la distance de la forme de chaque point de données.
Un modèle de relation linéaire peut être représenté mathématiquement comme ci-dessous:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Où,
β représente les caractéristiques
β 0 représente l'ordonnée à l'origine
β 1 représente le coefficient de caractéristique X 1
β n représente le coefficient de la caractéristique X n
Avantages et inconvénients de la régression linéaire
Vous trouverez ci-dessous les avantages et les inconvénients:
Les avantages
- En raison de sa simplicité, il est largement utilisé pour la modélisation des prédictions et des inférences.
- Il se concentre sur l'analyse et le prétraitement des données. Ainsi, il traite des données différentes sans se soucier des détails du modèle.
Désavantages
- Il fonctionne efficacement lorsque les données sont normalement distribuées. Ainsi, pour une modélisation efficace, la colinéarité doit être évitée.
Qu'est-ce que la régression logistique?
C'est une forme de régression qui permet la prédiction de variables discrètes par un mélange de prédicteurs continus et discrets. Il en résulte une transformation unique des variables dépendantes qui affecte non seulement le processus d'estimation mais aussi les coefficients des variables indépendantes. Il aborde la même question que la régression multiple, mais sans hypothèses de distribution sur les prédicteurs. Dans la régression logistique, la variable de résultat est binaire. Le but de l'analyse est d'évaluer les effets de multiples variables explicatives, qui peuvent être numériques ou catégoriques ou les deux.
Types de régression logistique
Voici les 2 types de régression logistique:
1. Régression logistique binaire
Il est utilisé lorsque la variable dépendante est dichotomique, c'est-à-dire comme un arbre à deux branches. Il est utilisé lorsque la variable dépendante n'est pas paramétrique.
Utilisé lorsque
- S'il n'y a pas de linéarité
- Il n'y a que deux niveaux de la variable dépendante.
- Si la normalité multivariée est douteuse.
2. Régression logistique multinomiale
L'analyse de régression logistique multinomiale nécessite que les variables indépendantes soient métriques ou dichotomiques. Il ne fait aucune hypothèse de linéarité, de normalité et d'homogénéité de variance pour les variables indépendantes.
Il est utilisé lorsque la variable dépendante a plus de deux catégories. Il est utilisé pour analyser les relations entre une variable dépendante non métrique et des variables indépendantes métriques ou dichotomiques, puis compare plusieurs groupes grâce à une combinaison de régressions logistiques binaires. Au final, il fournit un ensemble de coefficients pour chacune des deux comparaisons. Les coefficients du groupe de référence sont considérés comme étant tous des zéros. Enfin, la prédiction est effectuée sur la base de la probabilité résultante la plus élevée.
Avantage de la régression logistique: C'est une technique très efficace et largement utilisée car elle ne nécessite pas beaucoup de ressources de calcul et ne nécessite aucun réglage.
Inconvénient de la régression logistique: il ne peut pas être utilisé pour résoudre des problèmes non linéaires.
Comparaison directe entre régression linéaire et régression logistique (infographie)
Voici les 6 principales différences entre la régression linéaire et la régression logistique 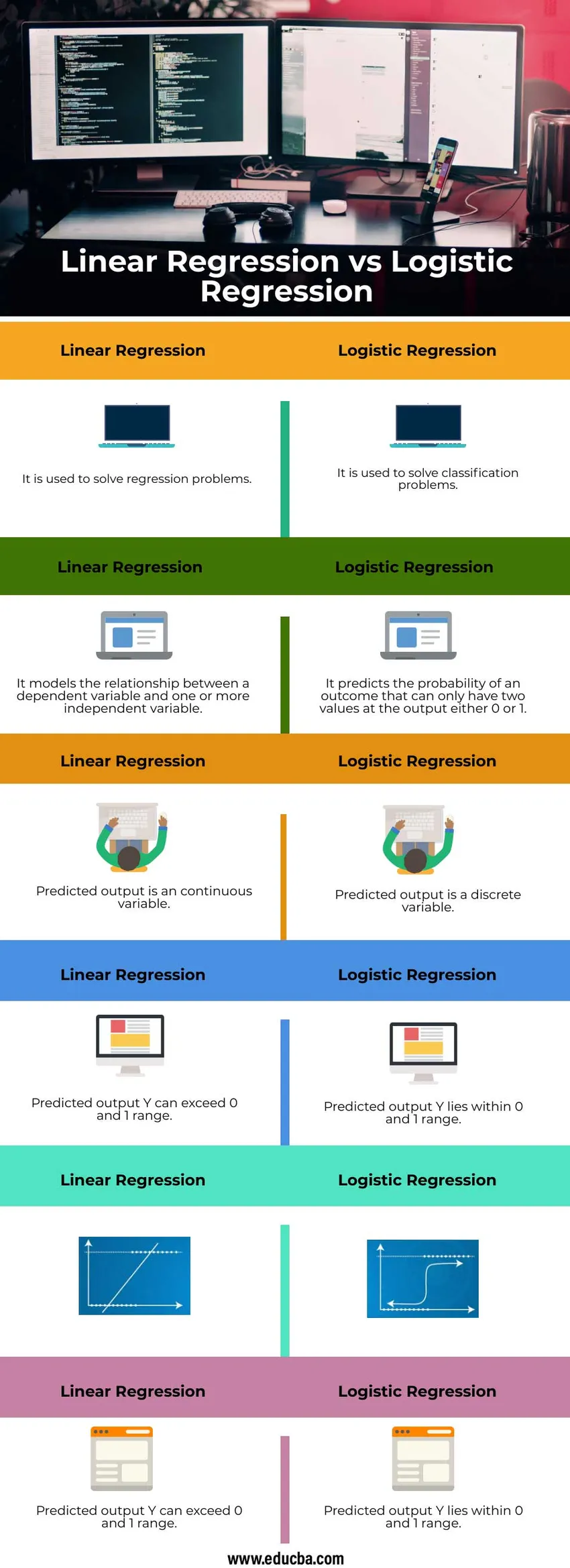
Différence clé entre la régression linéaire et la régression logistique
Laissez-nous discuter de certaines des principales différences clés entre la régression linéaire vs régression logistique
Régression linéaire
- C'est une approche linéaire
- Il utilise une ligne droite
- Il ne peut pas accepter de variables catégoriques
- Il doit ignorer les observations avec des valeurs manquantes de la variable indépendante numérique
- La sortie Y est donnée sous la forme
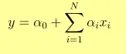
- 1 unité augmente de x augmente Y de α
Applications
- Prédire le prix d'un produit
- Prédire le score dans un match
Régression logistique
- C'est une approche statistique
- Il utilise une fonction sigmoïde
- Il peut prendre des variables catégoriques
- Il peut prendre des décisions même si des observations avec des valeurs manquantes sont présentes
- La sortie Y est donnée par, où z est donnée par
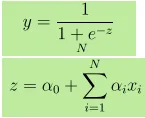
- 1 unité augmente de x augmente Y de log cotes de α
- Si P est la probabilité d'un événement, alors (1-P) est la probabilité qu'il ne se produise pas. Chances de succès = P / 1-P
Applications
- Prédire si aujourd'hui il pleuvra ou non.
- Prédire si un e-mail est un spam ou non.
Tableau de comparaison régression linéaire vs régression logistique
Discutons de la meilleure comparaison entre la régression linéaire et la régression logistique
|
Régression linéaire |
Régression logistique |
| Il est utilisé pour résoudre les problèmes de régression | Il est utilisé pour résoudre des problèmes de classification |
| Il modélise la relation entre une variable dépendante et une ou plusieurs variables indépendantes | Il prédit la probabilité d'un résultat qui ne peut avoir que deux valeurs en sortie soit 0 soit 1 |
| La sortie prévue est une variable continue | La sortie prévue est une variable discrète |
| La sortie Y prévue peut dépasser la plage de 0 et 1 | La sortie Y prévue se situe entre 0 et 1 |
 | 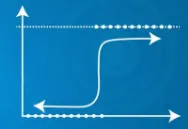 |
| La sortie Y prévue peut dépasser la plage de 0 et 1 | Sortie prévue |
Conclusion
Si les entités ne contribuent pas à la prédiction ou si elles sont très corrélées les unes aux autres, cela ajoute du bruit au modèle. Ainsi, les fonctionnalités qui ne contribuent pas suffisamment au modèle doivent être supprimées. Si les variables indépendantes sont fortement corrélées, cela peut entraîner un problème de multi-colinéarité, qui peut être résolu en exécutant des modèles séparés avec chaque variable indépendante.
Articles recommandés
Ceci a été un guide de régression linéaire vs régression logistique. Nous discutons ici des différences clés entre la régression linéaire et la régression logistique avec des infographies et un tableau de comparaison. Vous pouvez également consulter les articles suivants pour en savoir plus–
- Science des données vs visualisation des données
- Apprentissage automatique vs réseau neuronal
- Apprentissage supervisé vs apprentissage en profondeur
- Régression logistique en R