
Formule du coefficient de variation (table des matières)
- Formule
- Exemples
Qu'est-ce que la formule du coefficient de variation?
En statistique, le coefficient de variation également appelé CV est un outil qui nous aide à déterminer comment les points de données d'un ensemble de données sont répartis autour de la moyenne. Fondamentalement, tous les points de données sont tracés en premier, puis le coefficient de variation est utilisé pour mesurer la dispersion de ces points les uns par rapport aux autres et la moyenne. Cela nous aide donc à comprendre les données et à voir le modèle qu'elles forment. Il est calculé comme un rapport de l'écart-type de l'ensemble de données à la valeur moyenne. Plus le coefficient de variation est élevé, plus le niveau de dispersion des données autour de la moyenne est élevé. De même, plus la valeur du coefficient de variation est faible, plus la dispersion est faible et plus les résultats seront précis. Même si la moyenne de deux séries de données est considérablement différente, le coefficient de variation est très utile pour comparer le degré de variation d'une série de données à l'autre.
La formule du coefficient de variation est donnée par:
Coefficient of Variation = Standard Deviation / Mean
Étapes pour calculer le coefficient de variation:
Étape 1: Calculez la moyenne de l'ensemble de données. La moyenne est la moyenne de toutes les valeurs et peut être calculée en prenant la somme de toutes les valeurs, puis en la divisant par un certain nombre de points de données.
Étape 2: Calculez ensuite l'écart type de l'ensemble de données. C'est un petit processus qui prend du temps. L'écart type peut être calculé comme suit : √ (Σ (X i - X m ) 2 / (n - 1)) . X i est le ième point de données et X m est la moyenne de l'ensemble de données. Alternativement, nous pouvons également trouver l'écart type dans Excel en utilisant la fonction STDEV.S ().
Étape 3: Divisez l'écart type par la moyenne pour obtenir le coefficient de variation.
Exemples de formule de coefficient de variation (avec modèle Excel)
Prenons un exemple pour mieux comprendre le calcul du coefficient de variation.
Vous pouvez télécharger ce modèle Excel de formule de coefficient de variation ici - Modèle Excel de formule de coefficient de variationFormule du coefficient de variation - Exemple 1
Disons que nous avons deux ensembles de données A et B et chacun contient 20 points de données aléatoires. Calculez le coefficient de variation pour l'ensemble de données X et Y.
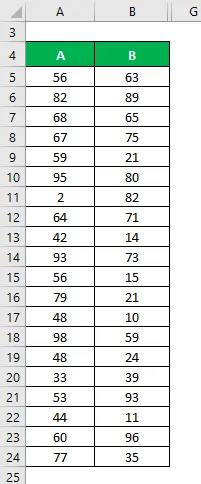
Solution:
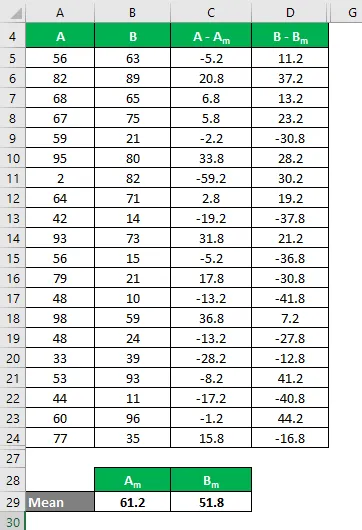
La moyenne est calculée comme suit:
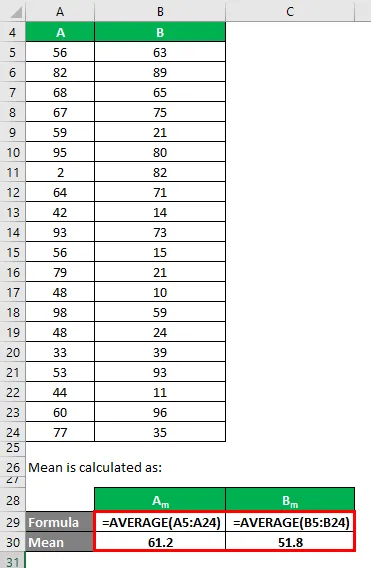
- Moyenne de l'ensemble de données A = 61, 2
- Moyenne de l'ensemble de données B = 51, 8
Maintenant, nous devons calculer la différence entre les points de données et la valeur moyenne.
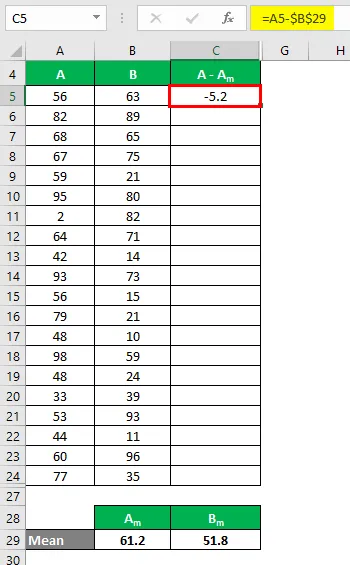
De même, calculez pour toutes les valeurs de l'ensemble de données A.
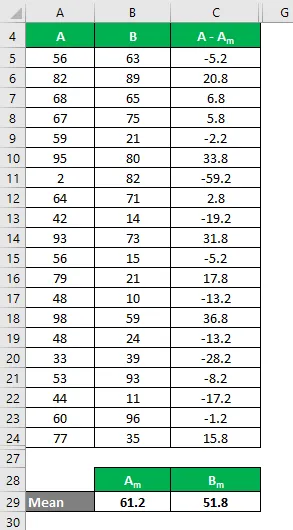
De même, calculez pour toutes les valeurs de l'ensemble de données B.
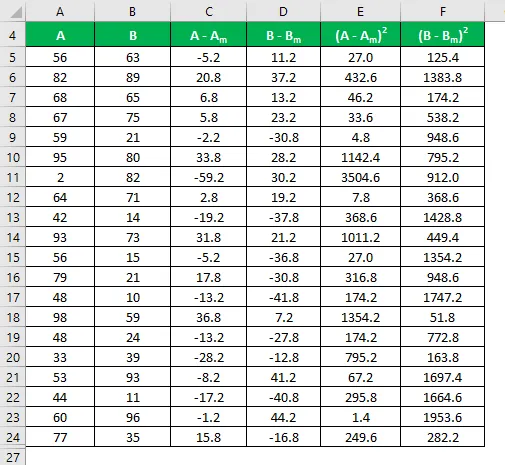
Calculez le carré de la différence pour les deux ensembles de données A et B.
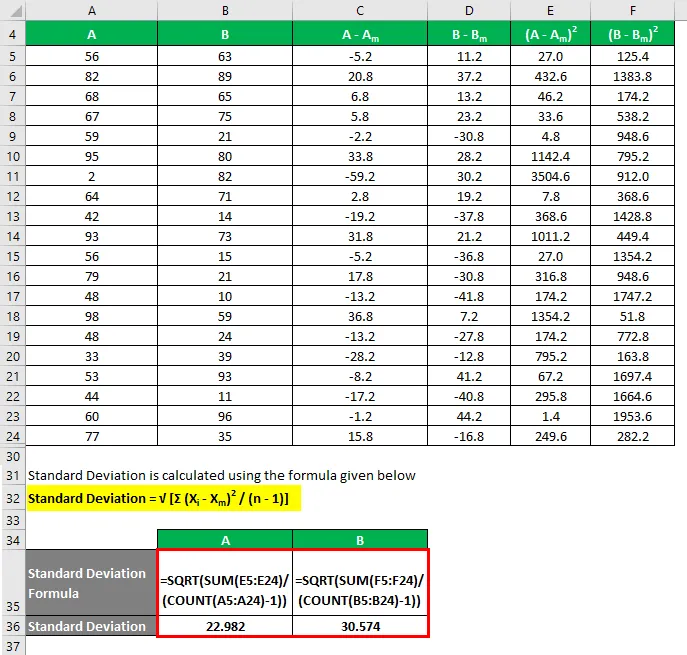
L'écart type est calculé à l'aide de la formule ci-dessous
Écart type = √ (Σ (X i - X m ) 2 / (n - 1))
Le coefficient de variation est calculé en utilisant la formule donnée ci-dessous
Coefficient de variation = écart-type / moyenne
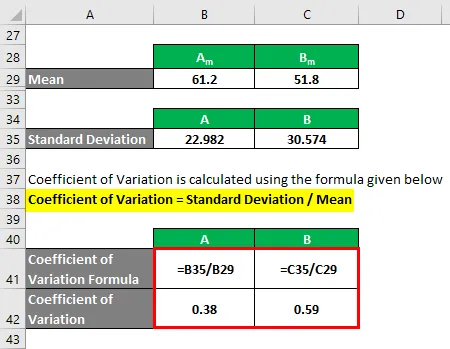
- Coefficient de variation A = 22, 982 / 61, 2 = 0, 38
- Coefficient de variation B = 30, 574 / 51, 8 = 0, 59
Donc, si vous voyez ici, B a un coefficient de variation plus élevé que A, ce qui signifie que les points de données de B sont plus dispersés que A.
Formule du coefficient de variation - Exemple 2
Disons que vous êtes un investisseur très peu enclin au risque et que vous cherchez à investir de l'argent sur le marché boursier. Étant donné que votre appétit pour le risque est faible, vous souhaitez investir dans des actions sûres qui ont un écart-type et un coefficient de variation plus faibles. Vous avez présélectionné 3 actions sur la base de leurs informations fondamentales et techniques et souhaitez choisir 2 actions. Vous avez également collecté des informations sur leurs retours historiques des 15 dernières années.
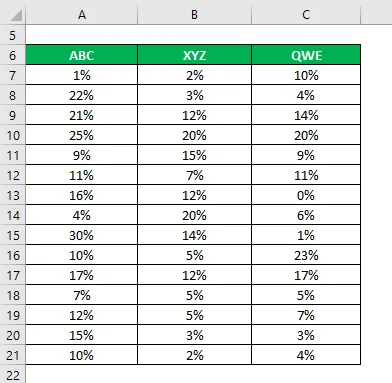
Solution:
La moyenne est calculée comme suit:
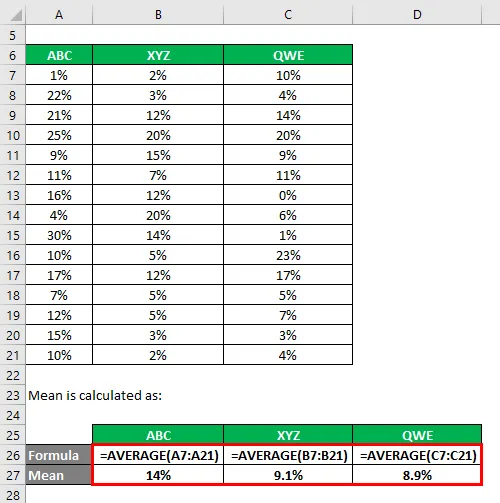
L'écart type est calculé à l'aide de la formule Excel
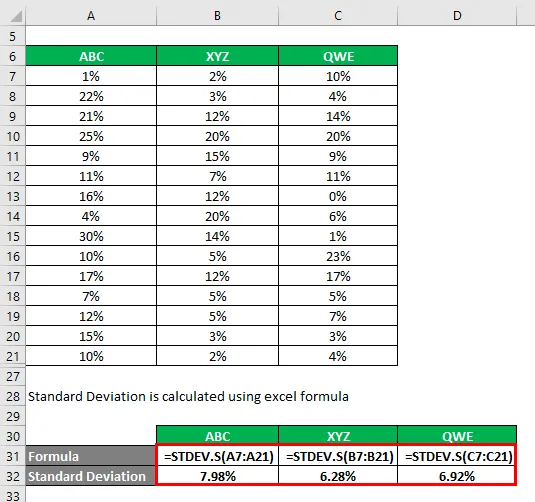
Le coefficient de variation est calculé en utilisant la formule donnée ci-dessous
Coefficient de variation = écart-type / moyenne
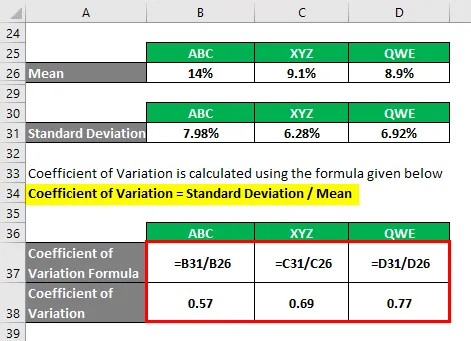
- Coefficient de variation ABC = 7, 98% / 14% = 0, 57
- Coefficient de variation XYZ = 6, 28% / 9, 1% = 0, 69
- Coefficient de variation QWE = 6, 92% / 8, 9% = 0, 77
Sur la base des informations, vous choisirez les actions ABC et XYZ à investir car elles ont le coefficient de variation le plus faible.
Explication
Le coefficient de variation étant une mesure du risque, il permet de mesurer la volatilité des prix des actions et autres instruments financiers. Il aide également les investisseurs et les analystes à comparer les risques associés aux différents investissements potentiels.
Le coefficient de variation est similaire à l'écart-type, mais un écart-type de deux variables ne peut pas être comparé pour être utile. Mais l'utilisation de l'écart-type et de la moyenne rend la comparaison relative plus significative. Il existe également une limitation du coefficient de variation. Supposons que la moyenne d'un ensemble de données soit nulle. Dans ce cas, cet outil deviendra inefficace. Non seulement cela, si nous avons un ensemble de données qui a de nombreuses valeurs positives et négatives, le coefficient de variation devient très problématique. Il n'est donc plus utile qu'avec des ensembles de données ayant le même signe plus-moins.
Pertinence et utilisations de la formule du coefficient de variation
Le coefficient de variation est pertinent dans de nombreux autres domaines que les statistiques. Par exemple, dans le domaine de la finance, le coefficient de variation est une mesure de risque. Il est similaire à l'écart-type car il est également utilisé comme mesure du risque, mais la différence est que le coefficient de variation est un meilleur indicateur du risque relatif. Par exemple, disons que le rendement attendu de A de 15% et le rendement attendu de B de 10% et A ont un écart type de 10%, tandis que B a un écart type de 5%. Pour choisir un meilleur investissement, le coefficient de variation peut être utilisé. Ainsi, le coefficient de variation de A est 10/15 = 0, 666 et le coefficient de variation de B est 5/10 = 0, 5. Donc B est un meilleur investissement que A.
Articles recommandés
Cela a été un guide pour la formule du coefficient de variation. Ici, nous discutons de la façon de calculer le coefficient de variation en utilisant une formule ainsi que des exemples pratiques et un modèle Excel téléchargeable. Vous pouvez également consulter les articles suivants pour en savoir plus -
- Qu'est-ce que la formule R ajustée au carré?
- Exemples de formule de coefficient de détermination
- Comment calculer le coefficient de corrélation à l'aide d'une formule?
- Formule de covariance avec modèle Excel